How to Create Your Own Windows Programs

CHAPTER 19

ICONS AND THE ICO FORMAT.

THE TECHNICALITIES OF ICON ENGINEERING:

Icons are fundamentally rectangular bitmaps but as, no doubt, everyone knows, an icon on the screen generally does not appear as rectangular because it can have parts of the bitmap that are transparent, which display the pre-existing background on which the icon is painted, even if this background is complex, and not all of a single colour. To achieve this, an icon is designed with a more complex structure than that of an ordinary bitmap. Since icons are universally present in all programs, I decided to give them a chapter of their own.

An ordinary device independent bitmap format requires a BITMAPINFOHEADER data structure, followed by a colour table, followed by an array of pixel colour indices into the colour table. If the array contains the actual colours, rather than the colour table numbers, there is no colour table, as one is not

needed.

In the case of an icon, the format is a little different. An *ico file, or an icon resource, can contain more than one icon image, and the file header is constructed to allow for this. In the ico format we will have an ICONDIR data structure, followed by ICONDIRENTRY data structures, one for each image, and all these are followed by the data for the icon images.

This image data, repeated for each icon image, will have a BITMAPINFOHEADER data structure, followed by a colour table, followed by an XOR mask, followed by an AND mask, which together constitute the image data for one image, and the image data for each successive image follows that of the previous image.

AND MASKS AND XOR MASKS:

It is necessary to describe, here, what AND and XOR masks are, and how they work together to paint an icon to the screen.

The structure of an icon involves the use of the programming equivalent of the binary gate principle we encountered in Chapter 2, and uses the AND and XOR forms. There are two parts to the pixel data of

an icon, one for use with an AND operation, and the other for use with an XOR operation, and these are referred to as the AND bitmask and XOR bitmask respectively. The 'mask' concept is supposed to give a sense of the 'gating' character of the operations, which filter the pixels that get printed or not printed to the screen.

THE AND MASK:

An AND operation, using the bitmask, is applied to the screen first, and the result of this is to turn all pixels on the screen, that will contain the visible icon pixels, to the colour black, which is the binary number zero, while allowing all the pixels that correspond to the transparent parts of the icon to remain unchanged. The AND operation achieves this as follows:

The AND bitmask operates as a gate that allows or blocks the appearance of pixel data on the screen. Where a bitmask pixel has the value 1, the corresponding pixel colour specification passes to the screen, whereas, where the bitmask pixel has the value 0, all data is blocked, and the pixel colour is set to zero, or black. This is consistent with the AND gate principle, in which a value of 1 opens the gate to allow data to pass through to the gate output, while a value of 0 blocks the data, so that the gate output remains at 0, whatever the data value on the input.

Thus, to create an AND bitmask, all the transparent pixels must be set to 1, and all the painted or non-transparent pixels must be set to 0.

In constructing an AND bitmask, you don't have to use the whole 24 bits of a colour value for each pixel, making them either all 1 or all zero. Instead, you set

only 1 bit for each pixel to either 1 or 0, and the icon reader automatically interprets this as 24 '1's or 24 '0's, for the purpose of specifying the icon painting operation.

This, of course, raises the programming question as to how you can set a single bit in either a register or memory variable, since all programming is based on bytes, or 8 bits, at least. Setting single bits thus has to be done indirectly, in the following way.

If you code 'mov eax,80h', you will set eax to the binary equivalent of 80h which, in 8 bits, is 10000000. This means that you have automatically set only the leftmost or highest bit of the al byte in the register. To set other bits within the al byte you can, for example, code 'shr eax,1', which will shift the value in the register to the right by 1 bit which, in the above case, gives the value 01000000, since the shr operation sets all the new bits to the left to zero. Thus, by shifting a single '1' bit one place each time, to correspond to each pixel, you can scan a succession of bits to represent 8 pixels. If you add the '1', (by simply adding al) to the AND bitmask, or not, each time, depending on whether the pixel is to be transparent or not, you can create '1's and '0's in a series corresponding to the icon image data.

THE XOR MASK:

Once the non-transparent icon pixels have been set to black on the screen, the XOR operation is used to print the icon pixels to the non-transparent areas, without printing anything to the transparent pixels.

The working of this operation is a bit more complicated than that for the AND mask in that, for the transparent pixels, the XOR bitmask acts as a gate switch, and the screen as the data, whereas, for the painted pixels, the black screen acts as the gate switch, and the bitmask as the data. This is like having a binary gate, with the first input acting as the gate switch, and the second as the data, and then suddenly switching the inputs, so that the first acts as the data, and the second as the gate switch. The reason for this method of working has its origin in the nature of the XOR operation.

An XOR binary gate, with two inputs, works such that, if either of the two inputs is 1, the gate output is 1 whereas, if both inputs are 0 or 1 together, the output is 0 (the difference between an XOR gate and an OR gate, by the way, is that an OR gate outputs a 1 if both inputs are 1, because it responds to a 1 on any input, even if other inputs are also 1).

The peculiarity, here, of the XOR circuit is that, if one input on the XOR gate is used as a gate switch, the gate cannot be simply opened or closed, as is the case with the AND gate, because setting the switch input to 0 or 1 will not 'open' or 'close' the gate, but will merely invert or not invert the data passing through the other input to the output.

What you can do with the XOR circuit, in the form of a gate, is to select which input data will pass to the output. If you hold one input at zero, the data from the second input will pass to the output and, if you

then hold the second input at zero, data can be passed from the first input to the output. Thus, if the XOR bitmask is on one input and the screen pixel data is on the other, where the XOR bitmask pixels are zero, the existing screen pixels will appear on the screen and, where the screen pixels are zero, the bitmask pixel data will be transmitted to the screen.

To correspond with this method of working, the XOR bitmask must have all the icon's transparent pixels set to zero, allowing the screen background data to get to the screen. Setting all the other XOR pixels to the values of the icon pixel's colour indices will then cause the corresponding screen pixels to be painted with the icon pixel colours. This is so because the painted icon pixels on the screen are all already set at zero by the AND operation, so that they then act as the gate switch, allowing the XOR bitmask painted, or non-transparent, pixels through to the screen. In this way the bitmask and screen alternately act as a gate switch or, more accurately, as the data source selector.

By these 'gate' descriptions I mean, of course, the software code emulation of the binary gate operations shown in chapter 2.

Let us recall, here, that, in the AND bitmask, each pixel needed to be represented by only 1 bit. In the case of the XOR bitmask, however, each pixel has to have the number of bits needed to describe the colour of the pixel, which is determined by the bit count of the particular bitmap colour format. The size, in bits, of the XOR bitmask is thus larger than that of the AND bitmask, though the number of pixels represented is the same.

SCANNING THE AND MASK:

There are particular, technical difficulties in properly reading from and writing to the AND mask of an icon, since this depends on an understanding of the method or algorithm by which AND mask bits are inserted into the AND mask array. There is more than one possibility, since the AND mask bits have to be dealt with in groups of at least 8 (one byte).

To develop the necessary understanding, we examine the following notational differences between the representations of the bits of data bytes, or words, or dwords, in registers or in memory variables.

We write the name of a register, such as eax, from left to right, which is thought of as the highest byte to the left, and the lowest to the right. But a memory location has the lowest byte to the left, at the location defined by the memory location name, and higher bytes towards the right. We could represent a register like eax in the same way, but this cannot be implemented in terms of the mov instruction. If, for example, I code:

mov eax, 112233h

I get the following

with the lowest byte, 33h, in al. So, we cannot code with the lowest byte to the left. If I code

mov [Address], dword 112233h

I get the following

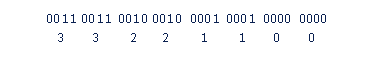
with the lowest byte, 33h, at the location defined by the name Address, which is then thought of as being on the left. If I now code

mov eax, [Address]

the order of bytes in eax is 112233h, with 33h in al.

Since these are just ways of describing the two cases, it would have been possible to reconcile and standardise these two viewpoints of registers and memory, but it is not normally necessary, since we

normally code in bytes rather than in bits. However, since we must code in bits for the icon masks, the usual way of thinking causes a complication that has to be observed. Whoever created the AND mask algorithm mixed these two views. The AND mask data is stored in memory, on a byte by byte basis, according to the second order, starting with a low address, but the bits within each byte are read and written according to the first order, starting with the highest bit and writing and reading towards the lowest. So you might have two AND mask bytes stored in memory as follows:

10011111 11101110

but each would be read from, or written to, the icon pixels as

11111001 01110111

In other words, in reading from, or writing to, the icon pixels, the order of the bytes relative to one another is preserved, but the order of the bits within each byte is read or written in reverse. So the bits as stored in the AND mask array do not represent the icon pixels continuously from start to finish. Instead, you jump to the 8th bit (the end of the first byte), read the bits backwards (high to low) one by one to the first, for the first 8 pixels, then jump to the 16th bit (the end of the next byte), and read backwards, one by one, to the 9th, for the second 8 pixels, and so on, jumping forward 16, and reading 8 backwards each time.

One may ask, why the complexity in such representations? This clearly appears to be a consequence of a partial lack of synchronisation between the original representations of registers and memory arrays. Whoever created the AND mask algorithm was thinking in terms of the representation from left to right in registers, which is the opposite to that in memory.

The upshot of all this is to say, in short, that the transparent and non-transparent pixel locations in the AND mask, within each byte, are affected by the manner in which they are written and read, such that the reading and writing algorithms must correspond.

This is a complication associated with the standard *.ico file format, which is necessary to consider only if you want to work with standard *.ico files. I discovered this complication only by trial and error, involving numerous failures until I eventually understood what was going on.

THE ANATOMY OF THE ICO FILE FORMAT:

As mentioned before, the ico file format has a different set of data structures than that of an ordinary bitmap file, although it also includes a BITMAPINFOHEADER structure like that of a bitmap. The following elements, successively inserted in the file, as listed down the page, describe the anatomy of an ico file containing a single icon image:

An ICONDIR data structure at the beginning of the file, followed by�
An IDONDIRENTRY data structure
A BITMAPINFOHEADER data structure
A COLOUR TABLE
An XOR mask
An AND mask

Examining these data structures individually, we have (note that the first column refers to the element offsets from the structure array name address, and the second column refers to the size, in bytes, of the structure element):

The COLOUR TABLE, which follows the above BITMAPINFOHEADER data structure consists of an array of dword colour values, with 24-bit rgb colour format, listing all the colours used in the particular icon. NOTE that icons, in the *.ico format, can have a maximum of 256 colours, so the colour table cannot be larger than 256 x 4 bytes, which is 1024, or 400h bytes. Each dword entry in the table has the form 00rrggbb, with rr gg and bb describing the values of the red, green, and blue colour components respectively.

The XOR mask, which follows the colour table is an

array of pixel colour no indices into the colour table, and the number of bits that describe the colour no depends on how many colours are in the table. A 256 colour icon requires one byte for each pixel, since one byte can count up to 0ffh, or 255, this being the number of the last table colour, if the first table colour has the number 0 (i.e. the colour numbers are zero based)

The AND mask, which follows the XOR mask, is an array of bits, with one bit corresponding to each pixel, as mentioned previously, set to 1 for transparent or 0 for non-transparent.

Part I: Part I Introduction
Chapter 1: Binary numbers, code, and procedures
Chapter 3: Assembly Language
Chapter 4: Assembly Language Code example
Chapter 5: Macros and HLA
Chapter 6: HLA code example
Chapter 7: The Windows operating system
Chapter 8: Data Structures
Chapter 9: How to Create a Windows Program
Chapter 10: How to Create an Exe File
Chapter 11: Structured Programming and OOP
Part II: Part II Introduction
Chapter 12: Debugging a Windows Program Code
Chapter 13: Painting the Window Client Area
Chapter 14: Creating Window Menus
Chapter 15: How to Create Toolbars
Chapter 16: How to Create Popup Menus
Chapter 17: About the Windows Clipboard
Chapter 18: How to Create Bitmaps
Chapter 19: Icons and the Ico Format
Chapter 20: Common Dialog Boxes
Chapter 21: Working with Files
Chapter 22: Scrollbars and Scrolling
Chapter 23: How to Send Data to the Printer
Chapter 24: Miscellaneous Topics

Material on this page may be reproduced
for personal use only.