How to Create Your Own Windows Programs

HOW TO CREATE YOUR OWN WINDOWS PROGRAMS

PART I

INTRODUCTION:

This programming work is divided into two parts. The first part is intended to introduce the reader, who may be unfamiliar with programming, to all the information necessary to understand what programming is, what the Windows operating system is, and how they relate to one another and to the underlying computer hardware. In addition, these general topics are selected, and dealt with, with a view to enabling the reader to gain an understanding of the design of the most basic possible Windows program, as quickly and easily as possible, sufficient to create a window and put it on the screen. The creation of the most basic possible Windows program thus ends part 1, except for a brief discussion of structured programming, in preparation for Part 2. The intention is to provide the basis for not only the creation of a basic windows program, but also for the discussion of further topics.

Part 2 relies on the preparation provided in part 1, and goes on to consider topics that will enable the reader to learn how to add particular features to the most basic program, that will then enable the creation of normal, useful programs. Since such extra features are, in the main, independent of one another, they tend to form self-contained topics that thus do not naturally suggest that they should be

presented in any particular order.

As mentioned, Part 1 ends with the general topic of structured programming. This may seem to be a rather advanced topic to introduce so quickly, but it is really unavoidable, due to its importance. Structured programming is a further development of the basic craft of programming, but is essential to facilitate the creation of programs of any significant size.

On first acquaintance, a reader new to programming may find the structured programming chapter hard to appreciate, not because it is intrinsically so complicated, which it is not, but because a lack of the practical experience of the problems that naturally arise in attempting to create programs. I suggest, however, that this should not give rise to any anxiety in a reader new to programming, and the chapter should initially be simply read for whatever illumination, little or much, that it might provide. Since later experience will serve to illuminate what initially might be obscure, I would emphasise that it should initially be at least read through and not skipped entirely.

CHAPTER 1

BINARY NUMBERS, CODE, AND PROCEDURES.

THE BINARY NUMBERING SYSTEM:

Our normal system for counting is the decimal numbering system, which has ten different numerical characters: 0,1,2,3,4,5,6,7,8,9. If we want to count beyond 9, we use pairs of characters, 10,11,12, etc., and then triplets, 100,101,102, etc., when we run out of pairs, and so on. There is nothing exclusive about such a system, and there can be other numbering systems, with different numbers of characters. A system with only six characters, 0,1,2,3,4,5, for example, would count as follows:

0,1,2,3,4,5, 10,11,12,13,14,15, 20,21,22,etc.

Thus, any numbering system switches to the use of pairs of characters as soon as it runs out of its individual characters. To have a numbering system with more than ten characters, we would have to invent some extra characters. The hexadecimal system, which is used by programmers, is an example, and uses six letters of the alphabet as extra numerical characters, and counts as follows:

0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f,10,11,12,13,14,15,16, 17,18,19,1a,1b,1c,1d,1e,1f,20,21…

Here we can see that, in the hexadecimal system, the number 10, where the use of pairs of characters begins, is equivalent to the decimal number 16 (hence the name hexadecimal). A numbering system with only two characters, 0 and 1, would count as follows:

0,1,10,11,100,101,110,111,1000,1001, etc.

This is the binary counting system, the word 'binary' indicating that it has only two characters. It would be a hopelessly cumbersome system to use for ordinary counting, but it is a perfectly suitable system to be adopted for use by a computer processor. This is the case because the transistors in a processor microchip, which are used to physically represent numbers, have a physically binary nature. This is explained in more detail in the following section, and in the next chapter.

HOW COMPUTERS USE A NUMBERING SYSTEM:

Transistors within the CPU (Central Processing Unit - or the 'brain' of a computer) have output terminals, each of which can have a voltage on it, or no voltage, which is a feature that is automatically binary in nature. Thus, zero voltage existing on a terminal can be taken to represent the numeral 0, and a voltage value can be taken to represent the numeral 1, which provides for transistor arrays to be used to represent binary numbers. In this way, a row of independent, transistor outputs can be used for counting, using the binary number system. Three transistors in a row, for example, can have their output voltages switched as follows:

000,001,010,011,100,101,110,111,

which is a binary count from 0 to 7. The CPU used in a Windows 32-bit operating system computer has rows of 32 transistors, using 32 outputs, and 32 outputs can be switched to count up to the binary number 11111111111111111111111111111111, which, in the decimal system, is the number 4,294,967,295, which is almost 4.3 billion. This dramatically illustrates that a numbering system with only two distinct characters can be used, without any difficulty, to manipulate very large numbers.

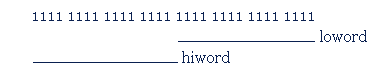
For convenience and flexibility, this 32-output array is given a series of names that refer to different parts of it, as follows (the 32 bits, or '1's, are printed here in groups of 4, just for extra clarity):

Thus, we can see that 'bit' refers to a single output, 'byte' refers to a group of 8 bits, 'word' refers to a group of 16 bits, or two bytes, and 'dword', or 'doubleword' refers to the whole 32 bits, or two words, or four bytes. A 32 bit array is sometimes also referred to in the following way, where 'loword' means the numerically lower word of the dword, and 'hiword' the numerically higher word of the dword.:

THE CPU AND MACHINE LANGUAGE:

The CPU is constructed with different 32-row sets of transistor outputs within its microchip, some of which are connected together in such a manner that rows of outputs with different particular numbers cause the CPU circuitry to operate in different ways. These are operating instruction values, rather than values being operated on, or used in calculations, because they control what the CPU is doing with the numerical values. One control value might, for example, instruct the CPU to add together two numerical values, while another might cause the result of the addition to be stored in memory, and so on. Since different control-type binary numbers are involved, in this way, in the functioning of the CPU, a series of such numbers, listed one after the other, can create sequences of operations within the CPU, which can be referred to as a sequences of code instructions, in this way creating what is normally referred to as a program's code. Such code, in binary form, is called 'machine language'. The microchip circuitry, and the code instruction numbers used by a programmer, were thus designed together to correspond to one another.

Apart from the CPU itself, there is also a memory bank consisting of an enormous array of binary outputs, called RAM (Random Access Memory), which is used to store information for the CPU to work on. This includes storage of all code instructions, for both the operating system itself and also the codes of individual programs. This memory bank exists in a set of microchips of its own, plugged, separately from the CPU, into the Motherboard or Mainboard, and connected to the CPU via several buses, a bus being a group of connecting wires printed onto the printed circuit board. This RAM memory is used only temporarily, when the computer is switched on, and is completely separate

from the computer permanent memory on the hard disk, where all files and permanent data are stored. The Windows Operating System is also permanently stored on the Hard Disk, but is automatically loaded into a reserved section of RAM memory when the computer is switched on.

This RAM memory bank is permanently connected to the CPU via the buses, but only those voltages representing a particular numerical value, within a particular, chosen memory location will be connected to the bus, and hence to the CPU, at any one time. This is accomplished by microchip circuitry referred to as a 'gate', with numbers of these gates forming the circuitry that connects a memory output to the bus. If all gates are 'closed', all the bus voltages are zero, and if specific gates are open, bus wire voltages are set by the voltage values coming through the open gates from the chosen memory location. So the bus wires carry the stored values to the CPU for the CPU to work on as needed.

From this it can be understood that there are always two separate numbers involved in memory operations, a gate number, which selects particular outputs within the memory array, and the number on the selected outputs. The gate number is called the memory 'address', and the number on the selected outputs is the number stored at that memory address. A similar arrangement feeds a number out of the CPU and into a selected memory location where it is to be stored. So the bus wires carry data out of RAM memory to the CPU, or from the CPU into RAM memory. Of course, reading a new value into a memory address will destroy the value already stored there. All this is explained in more detail in the section on cmos logic circuitry.

MACHINE LANGUAGE AND ASSEMBLY LANGUAGE:

It would be impossible, in practice, for any programmer to write programs directly in binary machine code. It would not, in fact, be impossible to write a section of code to begin with, but it would be a hopeless task to try to reread, recognise, and modify or correct code consisting of nothing but pages of binary numbers. Such code could be written in the form of hexadecimal numbers, which would be somewhat easier to read, but still virtually impossible to work with. Therefore, to make coding much easier, the instructions in binary form were converted

to much more easily recognisable words, by creating a compiler (assembler) that could translate an entire program composed of these words into binary code instructions to be directly used by the CPU. This set of recognisable words is what constitutes the programming language called Assembly Language. An Assembly Language programmer thus writes code in the form of such words, and leaves it to the assembler to translate it to machine code.

ASSEMBLY LANGUAGE AND OTHER COMPUTER LANGUAGES:

There is a variety of different computer languages other than Assembly Language, but these are so-called 'higher-level' languages (like C, C++, Java, Perl, etc.). That is because their code instructions do not relate directly to the CPU, as in Assembly Language, but actually represent entire blocks of Assembly Language. Their instructions are therefore like 'headings', (which is why they are called 'higher-level') inside of which are blocks of Assembly Language code, which are not accessible to the programmer. You understand Assembly Language by understanding how code instructions relate to the CPU and RAM hardware. To learn a higher-level language, without knowing Assembly Language, you have to learn a set of rules for writing instructions, without knowing the reason for them, or what such rules mean. This can be a serious disadvantage when it comes to understanding the inevitable faults that will occur in creating programs. Anyone who wants to create programs is therefore well advised to learn Assembly Language before using any other language or, perhaps, at least learn both together. In addition,

although higher-level languages can be written more quickly, they are also less flexible, since you cannot get access to the code within any of the individual instructions, and you may therefore need larger and more complicated code to do what Assembly Language could do more easily and directly.

It is worth mentioning that Assembly Language with Windows is far easier than pre-Windows Assembly Language, since the programmer no longer has to negotiate with hardware (like the monitor screen, or keyboard, etc.) by using interrupts (the 'int' code instruction), since all this is taken care of by the Windows Operating System. The Assembly programmer only has to use the Windows API (Application Programming Interface) Functions, which are the same functions that are used by all programming languages in the context of Windows.

This book therefore focusses on Assembly Language as its Windows Programming Language.

AN INTRODUCTION TO ASSEMBLY LANGUAGE:

Memory instructions:

Apart from direct instructions for the CPU, the programmer also uses words to define names of memory addresses in his program, and the assembler converts such names into binary numerical offsets relative to one another. The operating system then converts them to actual memory addresses when the *.exe file is loaded into memory. A programmer therefore has to declare or define such memory address names in a section of his code reserved for data declarations, and also declare how much of the memory (RAM, of course) is to be assigned to that particular name.

An address name, 'CHAR', for example, which refers to a byte sized address, can be defined in the data section of a program code as follows (db means 'byte', and 0 means that it is initialised to the value zero)

CHAR db 0

The system assigns a particular memory address to this name exclusively and also one byte of memory at this address and, wherever the programmer has used the word 'CHAR' throughout the program code, it is converted into the same particular memory address, which remains the same as long as the program is running. The programmer, therefore, doesn't have to be conderned about specifying, or obtaining, a particular numerical value for a memory address, and can always negotiate with a memory location by using its name only, leaving the system to take care of the actual numerical address value. The actual numerical value may be different each time the *.exe file is run, causing the program to be loaded from hard disk storage into RAM.

It has been mentioned that negotiating with memory always involves the use of two binary numbers, the first being the address, or gate number, and second being the actual value stored at the address. The code is designed so that the same name can specify either of these two numbers, as follows:

CHAR always refers to the address, or gate number

[CHAR] always refers to the numerical value stored at that address location.*

CPU instructions:

The CPU itself, as mentioned before, has a number of separate 32-bit output arrays which are also controlled by a binary 'gate' system, but this system is more complicated than the simple addressing system within the memory array, because the CPU arrays have to be connected together in numerous alternative ways to correspond to a variety of code instructions.

If the program code says 'add', for example, in Assembly Language, this instruction is translated to a binary number which, when connected into the CPU, operates via the wiring of the CPU gate system to produce a specific result. If eax and ebx are the names of two 32-bit CPU arrays, for example, and the code contains the following instruction:

add eax,ebx

the binary numbers in the instruction, into which this is translated, cause the CPU to add the binary number in the 32-bit array ebx to the binary number in the array eax to produce the equivalent of the equation

eax = eax + ebx

which means that the result of the addition modifies the value in eax, but not inebx. If you were to write

add ebx,eax

The equivalent equation would be

ebx = ebx + eax

so the result modifies the value in ebx, and not in eax.

There is thus a set of instructions wired into the gate system of the CPU such that the program code can tell it to carry out a variety of operations.

The CPU code instructions, the addresses of the code instructions, the values being operated on, the values stored in memory, and their memory addresses, are all in the form of binary numbers. This binary based design principle also enables the CPU to receive input from a keyboard or mouse, and send output to a video screen or printer, and every detail, and every operation is defined and carried out by means of numbers in binary form.

If, for example, a user presses the key 'a' on the keyboard, this generates the binary equivalent of the decimal number 97. This number is used by the CPU to select the number 97 bitmap from a font and print the bitmap pixels, as defined by the font, to the video screen, where both the individual pixel colours, and the location of the bitmap on the screen, are also described in the form of numbers in binary form.

When an *.exe file is run, and loaded into memory, its code is loaded into a particular memory block in RAM, assigned by the operation system to be used by the code only, and not for any other purpose. The gate or addressing system, in relation to this code, is operated by a special 32-bit array in the CPU, called the Instruction Pointer, also called eip, and this Instruction Pointer automatically begins at the address at the start of the program code. The CPU responds to the instruction code at this address, and then increments the address number in the Instruction Pointer in order to get the next code instruction. It automatically continues to do this until the Instruction Pointer reaches the end of the code.

The way in which a program, or the operating system itself, prevents the Instruction Pointer running off the end of the code is by means of instructions that can cause the Instruction Pointer to jump back to addresses in previous parts of the code. While the computer is on, the CPU Instruction Pointer is therefore always running around all kinds of code loops, and from one loop to another, in the program or operating system code, and never exits all the code until an instruction tells the system to shut down.

There is already enough in this introduction to enable us to examine a simple piece of code but, at the same time, introduce a very important way of writing selfcontained segments or blocks of code, which are constantly used in programs, and also in the Windows operating system.

There is an instruction 'mov', written in the code as mov eax, for example, which tells the CPU to 'move' a value into the eax 32-bit array. The complete instruction, on a single line, would be something like one of the following alternatives

mov eax,10
or
mov eax,LengthA
or
mov eax,[LengthA]
or
mov eax,ebx

The first alternative tells the CPU to move the value 10 into eax, the second tells it to move the binary value of the address named LengthA (not its contents) into eax, the third tells it to move the value stored in the address LengthA (its contents) into eax, and the last tells it to move the value in ebx into eax.

Now let us write

mov eax,[LengthA]
mov ebx,[LengthB]
add eax,ebx
mov [LengthC],eax

If the values stored in all these addresses are binary numbers for different lengths (possibly of blocks of land, or whatever), for example, the code tells the CPU to get the length values out of memory addresses LengthA and LengthB, add them together, and put the result in the address LengthC. From the last instruction you can see that you can write mov [LengthC],eax, just as well as you can write mov eax,[LengthC]. There is, of course, a set of instructions that allows you to instruct the CPU to carry our a variety of other operations, as we will examine further on.

THE UNIVERSALLY IMPORTANT CONCEPT OF PROCEDURES, SOMETIMES ALSO CALLED FUNCTIONS, OR SUBROUTINES:

The above section of code allows us to examine the concept of self-contained blocks of code which I mentioned. In just the same way that a memory location in the ordinary data storage section of RAM is able to be indicated by a name like LengthA, a memory location in the code segment of memory can also by indicated by a name, and this is done by simply writing the name as a line in the code, as follows:

AddLengths:
mov eax,[LengthA]
mov ebx,[LengthB]
add eax,ebx
mov [LengthC],eax

'AddLengths' is now the name that is given to the address of the code instruction immediately following, i.e. mov eax,[LengthA]. There are instructions that make use of this, and one of them is the 'jmp' instruction (short for 'jump'). If I write a line of code somewhere else in my code, as follows:

jmp AddLengths

it will tell the CPU to move the Instruction Pointer to the address indicated by AddLengths, which means that the Instruction Pointer will jump to the above code and run through it, starting at the instruction mov eax,[LengthA]. Now consider the following code:

AddLengths:
mov eax,[LengthA]
mov ebx,[LengthB]
add eax,ebx
ret

You can see that a 'ret' (return) instruction has been added to the end of the code. Such a ret instruction is for use in conjunction with a 'call' instruction, which is used instead of a 'jmp' instruction. Thus, if I write

call AddLengths

the Instruction Pointer will jump to the address AddLengths, as with a jmp instruction, but, when it reaches the ret instruction, it will jump back (return) to the line of code just after the instruction 'call AddLengths'. Suppose, therefore, we have the following piece of code:

mov [LengthA],ecx
call AddLengths
mov eax,[LengthC]

(ecx is another 32-bit CPU array, like eax and ebx). What happens here is that the binary length value in ecx is put into the address LengthA, the Instruction Pointer jumps to the code address AddLengths, runs through the code, until it reaches the ret instruction, and then jumps back to the instruction immediately following the call, i.e. mov eax,[LengthC].

Here, the piece of code between the AddLengths address and the ret instruction is what I called a self-contained segment, or block of code.

It can be called many times, from different parts of the code, if required, and always jumps back to the place from where it was called, which means that this block of code can be used many times without having to be written out in full on each occasion.

How the CPU does this is that, on encountering the 'call' instruction, it saves the address of the instruction immediately following the call instruction and, when it meets the ret instruction, it puts the saved address back into the Instruction Pointer, so that the Instruction Pointer is immediately back at the address after the call instruction. The above self-contained block of code is referred to as a PROCEDURE, or sometimes, also, as a FUNCTION or SUBROUTINE, and the procedure is given the name of the starting address, i.e. AddLengths is the name of the procedure in the above example.

Procedures are of the highest importance, and are used all the time, and it is by calling procedure names that a program's code is enabled to interact with the Windows operating system code, and vice versa. The Windows API (Application Programming Interface) Functions are names of procedures whose code is within the operating system, and not visible to the programmer.

This works because you can call a procedure name even if you don't know what the actual code is inside the procedure and, indeed, Microsoft does not allow anyone outside to know the internal working of the Windows code, and gives a programmer only the procedure names to work with. The collection of Windows procedure names available to the programmer to use is referred to as the Windows API, or Application Programming Interface, as mentioned already.

*A NOTE ON ASSEMBLY LANGUAGE COMPILERS, OR ASSEMBLERS:

A piece of Assembly Language code has a definite syntax which must be adhered to for writing instructions. Syntax is like the correct programming 'grammar' that the compiler or assembler needs to be able to read the code and translate it to binary machine language. Different Assembly Language compilers, or assemblers, generally have basically the same syntax as one another, but there will be some small differences between them, so that code written for one assembler will not be correctly translated by a different assembler. The differences usually involve differences in syntax for declaring

memory addresses and associated blocks of memory, or in specifying the memory size to be used in individual code instructions. There will also be differences in the codes used for macros (macros will be described later on).

ALL ASSEMBLY LANGUAGE INSTRUCTIONS USED IN THIS WORK ARE BASED ON THE SYNTAX ASSOCIATED WITH THE NASM FREEWARE ASSEMBLER, WHICH CAN BE DOWNLOADED FREE FROM THE NASM WEBSITE.

Part I: Part I Introduction
Chapter 1: Binary numbers, code, and procedures
Chapter 3: Assembly Language
Chapter 4: Assembly Language Code example
Chapter 5: Macros and HLA
Chapter 6: HLA code example
Chapter 7: The Windows operating system
Chapter 8: Data Structures
Chapter 9: How to Create a Windows Program
Chapter 10: How to Create an Exe File
Chapter 11: Structured Programming and OOP
Part II: Part II Introduction
Chapter 12: Debugging a Windows Program Code
Chapter 13: Painting the Window Client Area
Chapter 14: Creating Window Menus
Chapter 15: How to Create Toolbars
Chapter 16: How to Create Popup Menus
Chapter 17: About the Windows Clipboard
Chapter 18: How to Create Bitmaps
Chapter 19: Icons and the Ico Format
Chapter 20: Common Dialog Boxes
Chapter 21: Working with Files
Chapter 22: Scrollbars and Scrolling
Chapter 23: How to Send Data to the Printer
Chapter 24: Miscellaneous Topics

Material on this page may be reproduced
for personal use only.