AN AETHER FLOW MODEL OF GRAVITATION

Since first coming across the Schwarzschild Solution to Einstein's gravitational equations in General Relativity, I have always been intrigued by a series of coincidences that appear to be, as it were, far too coincidental.

Firstly, the Schwarzschild solution has the form of a modified Minkowski equation, in which the modifying factor has a form identical to gamma in Special Relativity - a notable coincidence. The time modifying factor in the gravitational time dilation equation is also identical in form to gamma in Special Relativity, and also identical in all respects to the modifying factor in the Schwarzschild solution, which is a second notable coincidence. Furthermore, what corresponds, in this modifying factor, to a velocity in gamma, is identical to the escape velocity of a test object within the gravitational field, which is a third remarkable coincidence.

Consequently, since becoming aware of this, I have been of the view that there is likely to be some way of linking all these similarities together into a single picture that would show that the apparent coincidences are really just different manifestations of a common reality underlying all of them.

Here, I intend to propose an argument to identify what this underlying reality might be, and what

might be the working of the mechanism, in the gravitational field, that achieves it. This will be a version of the so-called 'river model of gravitation', which I have called an 'aether flow model of gravitation', forms of which have already been investigated by others, as indicated in the next section.

My version will involve a different approach, will make use of light trajectories as defined by Special Relativity Light Theory, not the standard spacetime version, combined with a concept of a flowing aether, used to account for both gravitational and acceleration time dilation by means of an identical mechanism, in keeping with Einstein's principle of equivalence between both of these. This will include the necessity to find a solution for the problem posed for special relativity by the concept of an aether.

All this will then be used as the basis of the mechanism that modifies the Minkowski time dilation equation of a small orbiting test object, in order to produce an equation identical to the Schwarzschild solution to the gravitational equations in General Relativity, but without making any reference at all to that theory. This will demonstrate that the Schwarzschild equation can be obtained solely on the basis of special relativistic corrections to ordinary Newtonian gravitation.

SUMMARY

The 'coincidences' I mention in the previous section have been noticed already by others, who made attempts to create what has recently been called the 'River Model' of gravitation. That is, equations similar to the Schwarzschild equation in GR can be constructed if one supposes that space is moving inward past the orbiting body at the Newtonian escape velocity at each elevation in the field. The idea for such a model of gravitation began with Allvar Gullstrand and Paul Painleve, in the 1920's, in the Gullstrand-Painleve metric. Andrew Hamilton and Jason Lisle have used this metric to create what they call the 'River Model of Black Holes'. Reginald Cahill has also created a version he calls the '3-Space In-Flow Theory of Gravity'

I shall not refer, in my interpretation of the river model idea, to the work of these and others, since I

have not approached it in the same way, and have not formed what follows as a development or extension of their work. To refer to it would therefore pointlessly complicate the following description. Furthermore, what I shall say depends on the interpretation of Special Relativity as a theory of Light and not on the spacetime theory (follow the link to see the original page on this).

"The River Model of Black Holes" by Andrew J. S. Hamilton and Jason P. Lisle arXiv:gr-qc/0411060v2 31 Aug 2006

"3-Space In-Flow Theory of Gravity: Boreholes, Blackholes and the Fine Structure Constant" by Reginald T. Cahill arXiv:physics/0512109v1 [physics gen-ph] 13 Dec 2005

PREVIOUS EFFORTS TO CREATE A RIVER MODEL OF GRAVITATION:

The fundamental concept of a river type model of gravitation involves an inward flow towards the centre of the gravitational field. We must therefore consider two possibilities:

1) That space itself is flowing inward towards the centre of the field. This option might seem to avoid the problems involved in dealing with some content of space, rather than space itself only.

2) That some content of space, such as an aether, is flowing inward towards the centre of the field, but the space itself is considered to be stationary.

While the aether concept is thought to be problematic in Special Relativity, the concept of a flowing space is no less problematic, as I will discuss in the next section.

THE FUNDAMENTAL CONCEPT INVOLVED IN A RIVER MODEL OF GRAVITATION:

The concept of a 'moving' or 'flowing' space must be properly examined in order to see how it can be made credible to the understanding. What, after all, could be meant by saying that empty space is 'moving'? I cannot propose that as an intelligible concept in that I can conceive only some content of space as 'moving'.

From the beginning, the concept of motion has always been, and always still is, associated with some content of space, the motion of which, relative to some other content of space, can be identified. There is really no concept, and never has been, of space itself as something that can demonstrate motion. It appears necessary, therefore, to identify the concept of an inflow as defining a gravitational field as being really an inflow of some kind of substance within space, which I shall call an aether, for want of a better description. I have consequently referred to this concept, in the page title, as an 'aether flow model of gravitation'.

Such a concept of an inflowing aether, however,

would suggest that space, as a whole, is filled with an aether, which is normally stationary, but flows inward in the region of a gravitational source (or sink, more accurately). We therefore have a resurrection of all problems associated with an aether being involved in Special Relativity. We have to face the problem relating to the reference frame of such an aether, since this would appear to set up an absolute motion of frames in an aether, apparently contradicting the simple relativity of the motion of inertial reference frames relative to one another. We will deal with this problem in the next section.

There is another problem that arises in respect of an inflowing aether, which I will deal with in a later section, and that is that, if an aether is a substance of any kind, and flows inwards towards a centre from all directions, there must be some mechanism to dispose of the accumulated substance so that it does not have to be considered to accumulate in an unlimited quantity forever.

THE PROBLEMATIC CONCEPT OF A MOVING SPACE:

The problem created by the possible reference frame of an aether is, in fact, not really a peculiarity specific to the concept of an aether, because it applies also to space itself, even if it is thought to contain no aether.

What, for example, could be identified as the reference frame of space itself (whether we mean 3 dimensional space, or 4-dimensional spacetime) in Special Relativity? How can one avoid this question, since space is considered to be a single arena (like a reference frame) which contains many reference frames in motion relative to one another?

To answer this we must try to answer the question: 'how might the reference frame of space itself be defined within Special Relativity?'

Let us suppose, as usual, that no inertial frame has a privilege in defining the reference frame of space itself. In other words, all inertial frames must be given equal status in defining the space they occupy. This inevitably means that each inertial observer will define himself to be stationary in the space within his own frame. If all inertial observers may do this, irrespective of their relative motions, it follows that each inertial frame is being specified to have its own space, which is also in motion relative to the space within all other inertial frames. (Although this appears to confer motion on empty space, contrary to what was argued previously, it is not really a motion assigned to space itself, but only something

indirect, which is logically implied by the motion of some content of space, with which the motion is directly associated).

How could this be possible? Would each inertial frame be dragging a region of space along with itself relative to other inertial frames? This could not make sense in that the simple definition of space is that it is limitless in all directions. In fact, the only way in which each three dimensional inertial frame could define a limitless space in which it is stationary is if all inertial frames, in relative motion, were able to occupy separate three dimensional spaces displaced relative to one another in a fourth physical dimension. In such a scenario, it would be quite possible for each such space to be filled with an aether, in which case every inertial frame will contain its own limitless, stationary aether, in motion relative to the limitless, stationary aether of every other inertial frame.

I shall therefore adopt this viewpoint, which allows us to have both the existence of the aether, and the absolutely relative motion of inertial frames. Each inertial frame then consists of a thin three dimensional slice of a physically higher dimensional space. I specify that it must be 'thin' in order that the higher dimensional physical displacement of one inertial frame relative to another may be too small to have any ordinary geometrical significance.

SPACE, OR AN AETHER, IN SPECIAL RELATIVITY, AND
THE PROBLEM OF IDENTIFYING ITS REFERENCE FRAME:

Since every inertial frame occupies its own 3 dimensional space, and there are 3 orthogonal directions within such a space, there must therefore also be 3 different orthogonal displacements possible in the higher dimensional physical space ( i.e. excluding the time direction). This is because a single higher dimensional displacement cannot represent a particular relative velocity of inertial frames in two or three orthogonal directions. This requires a separate displacement to be possible for each of the three orthogonal directions in 3-D space. We must thus have an inertial frame existing as a thin 3-D section of a six-dimensional physical space, so that, if we include time, we must have a seven dimensional spacetime. Only 4 dimensions, including time, can have geometrical significance, as mentioned before. The following diagram illustrates this situation:

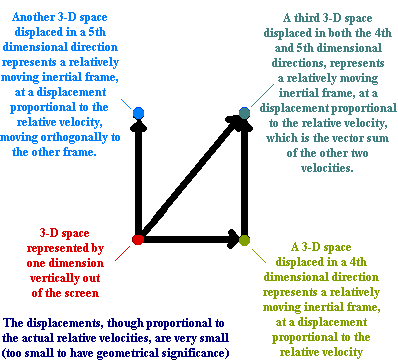
THAT THE ARGUMENT IN THE PREVIOUS SECTION REQUIRES
THAT SPACETIME MUST HAVE MORE THAN FOUR DIMENSIONS:

We have selected a postulate that each relatively moving inertial frame has its own aether that is stationary with respect to itself. The conception of gravitation as an aether flow will consist of the fact that any mass causes a flow of this aether towards its own gravitational centre. For a relatively very small mass, this aether flow will be significant only within a very small region close to the mass centre of gravity, with the rest of its aether being effectively regarded as stationary. For a very large mass, however, the aether flow will be significant over a much wider volume of space around its centre of mass.

For the purpose of establishing the concept of gravitational force as based on an aether flow, we must now postulate that the aether flow of a very massive body, like a planet, is able to influence the stationary aether of a small mass.

If the small mass is not allowed to be in radial free fall towards the centre of the large mass centre of gravity, this influence of the large body aether flow will be such as to introduce a component of flow of the aether of the small body in tandem with itself, and this aether flow thus created within the normally stationary aether of the small mass causes a relative motion between the small mass and its own aether, and this will constitute the basis of the gravitational force exerted on the small body.

The transmission of energy to such a small mass, if it is allowed to commence falling in response to this gravitational force, will be quantised, which means that such transmission of discrete quanta of energy will take the usual form of some kind of bosons (gravitons).

The relative motion between the small mass and its own aether also establishes the inertial response of the small mass, which consists of a tendency of the small mass to be at rest with respect to the spherically symmetrical flow of its own aether towards itself (which constitutes its own gravitational field), and it therefore resists any distortion of this flow in order, if possible, to restore the normal state of rest between itself and its own aether.

In order to include Einstein's Principle of Equivalence between a gravitational force on a small body and an ordinary accelerating force applied to the small body by other means, we shall postulate that any kind of force applied to the small body also causes a temporary relative motion between the body and its own normally 'stationary' aether, which produces the same resistance to this distortion of the relationship between the small mass and its own aether, resulting in the same inertial response, or opposing force, mentioned in the previous paragraph.

Any reference to the 'stationary' aether of a small mass, or the mass being 'at rest' relative to it, ignores the very small, spherically symmetrical aether flow within the small mass aether, which constitutes its own very small gravitational field, and signifies that fact that there is normally no overall relative motion between this symmetrical aether flow, as a whole, and the small mass itself.

We must now consider how this picture of reality involving an aether relates to the bosons of the electromagnetic field (photons).

THE AETHER FLOW MECHANISM OF GRAVITATION:

In Special Relativity as a Theory of Light, light appears as a multicomponent reality, involving separate 'foci of propagation', each travelling at velocity, c, within all possible inertial frames. These foci of propagation are locations at which a photon can appear, and not simply photons as such. It is not possible, therefore, to simply suppose that photons use the aether associated with a body as simply a medium for their transmission, like waves in water, for example. But what follows here makes it necessary to suppose some link between photons and the aether of a body. I will therefore postulate that a focus of propagation always travels at velocity c, the velocity of light, in accordance with the light postulate of SR, relative to any body with which it interacts but, at the same time, cannot be considered to travel independently of any aether.

The focus of propagation that represents this motion of a photon in an object's own inertial frame I will call the 'proper' focus of propagation (see illustration section below), to distinguish it from foci of propagation of the same photon in other inertial frames. The significance of a proper focus of propagation is that it expresses the motion of photons that determine the rate of internal working of any body, such as that of a clock. This gives it a prior or principal significance in that it forms the basis for the time dilation effects of all other foci of propagation in all other inertial frames. It is also the case that such proper foci of propagation travel at velocity c relative to both the body and its own aether, since these are both at rest within the same inertial frame (with the concept of an aether 'at rest' having the meaning previously discussed).

From this viewpoint, the relative motion between a body and its own aether, whether caused by an external gravitational field, or by acceleration, causes a problem for the concept of a proper focus of propagation in that there is no longer any aether at rest with respect to the relevant body or clock mechanism, so that the normal rule determining the proper focus of propagation can no longer apply.

If, as previously suggested, a focus of propagation cannot travel independently of any aether, and a body in a gravitational field has no aether stationary with respect to itself, it follows that the normal proper focus of propagation cannot exist in the

reference frame in which the body is stationary. The focus of propagation must travel within the moving aether, notwithstanding it must travel at velocity c relative to the body itself. This results in the foci of propagation acquiring the same form as those in a stationary frame that result from the normal proper foci of propagation existing within a moving frame.

If we now consider a reference frame co-moving with the body's aether, which is moving relative to it due to the presence of the gravitational field, and is stationary in the aether, the body itself will be moving within this frame, so that a focus of propagation seen to be oscillating within the body will also be seen to have the form of a stationary frame focus of propagation.

So, the result is that when an inertial object, with internal foci of propagation of light as part of its internal structure having the normal form of proper foci of propagation, is introduced into a gravitational field, which causes a relative motion to develop between the object and its own aether, the form of the trajectories of the normal foci of propagation will become dragged out of shape by the relative motion, in a manner that conforms to the light postulate of SR, and will acquire the forms of stationary frame type foci of propagation, in a reference frame in which the body is stationary, and in a reference frame co-moving with the body's moving aether (see the illustrations section below)

In this situation, the object (let us say it is a clock), has no foci of propagation that do not have the stationary frame type of form. Since a stationary frame focus of propagation oscillates more slowly than that of a normal proper focus of propagation, the result will be a slowing of the rate of the clock. A consequence is that a stationary frame time dilation effect is incorporated into the actual, physical working of the clock in the gravitational field (or, equivalently, under the influence of any ordinary accelerating force).

Since the time dilation effect is incorporated into the working of the clock, which is not the case with relatively moving inertial frames, it will have a real, permanent, cumulative effect on the reading of a clock.

THE AETHER FLOW MECHANISM OF GRAVITATIONAL TIME DILATION:

ILLUSTRATIONS:

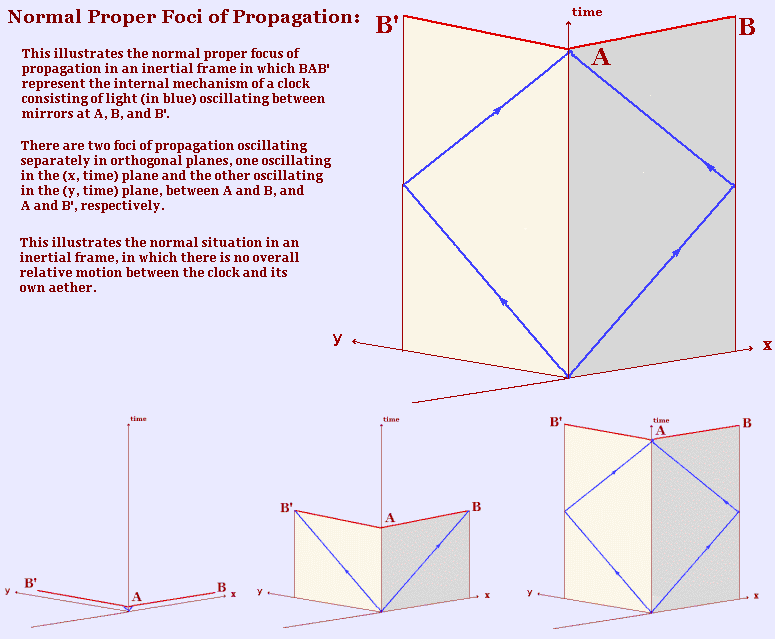
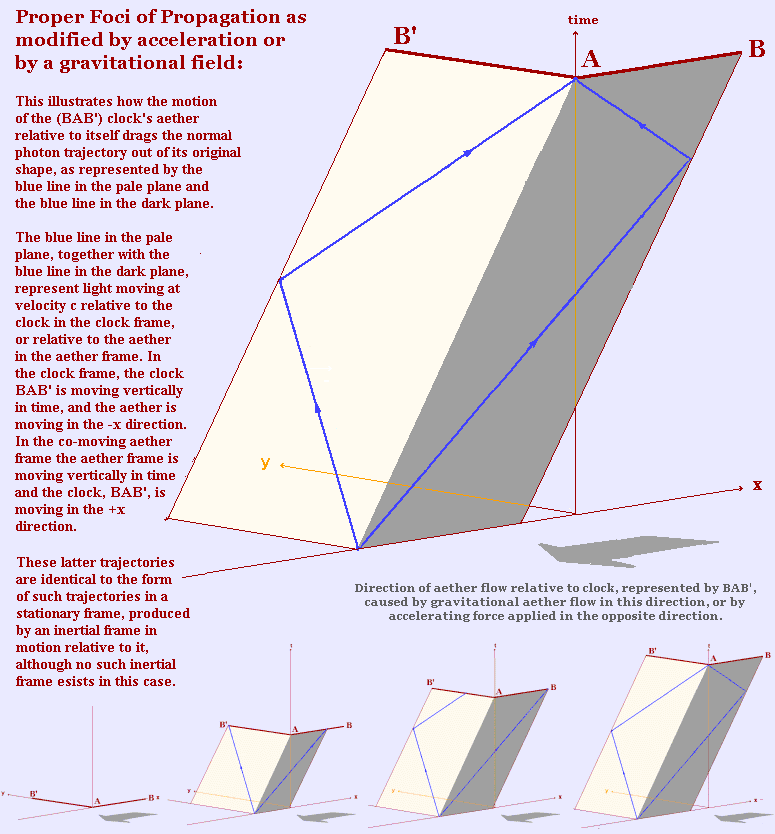
As is well known, a clock stationary in a gravitational field is time dilated compared to a clock outside the field, the value of the time dilation being given by the equation

t_f = t_o(1-2GM/rc²)^1/2,

where t_f is in the field and t_o is outside of it.

If we specify gamma, as in Special Relativity, as (1-(v/c)²)^1/2, then (2GM/r)^1/2, in the equation, corresponds to a velocity, v, in a gamma value in Special Relativity, and the equation is similar to the Special Relativitistic time dilation equation

t_f = t_o(1/γ).

The escape velocity of an object in a gravitational field is that velocity that will give the object just enough Kinetic Energy to climb out of the field against the field's potential energy, which is also the velocity an object would acquire by free falling to that part of the field if starting at zero velocity from outside it. This velocity is given by an equation relating the Kinetic Energy to the gravitational potential energy difference between the radial location within the field and outer space, outside the field. This equation is

(1/2)mv² = GMm/r

giving a velocity

v = (2GM/r)^1/2

Remarkably, this velocity is the same value as that which corresponds to the velocity in the gravitational time dilation equation referred to above. It is possible, therefore, to create the postulate (as we have done) that an inflowing aether, which constitutes the gravitational field, has this velocity, as determined by each particular value of the radial distance from the centre of gravity. In other words, at a radial distance, r, from the centre of the field, the gravitational time dilation factor IS a Special Relativistic gamma value, with (2GM/r)^1/2 as an actual velocity.

1/(1-2GM/rc²)^1/2 is therefore the special relativistic equivalent gamma value. The clock physically slows only because its own aether is in relative motion to itself, as described already, which is equivalent to a Special Relativistic mechanism, just as it is in the case of acceleration. That is, the photons, or electromagnetic bosons, internal to the working of the clock mechanism, are oscillating, more slowly than normally, in the equivalent of a 'stationary' inertial frame as has been described already.

THE CALCULATION OF GRAVITATIONAL TIME DILATION:

The aether flowing inward towards the centre of a gravitational field must have some means of exiting from the field in order to avoid an unlimited accumulation of the aether at the centre of the field. Not only that, but there is also the problem that the total quantity of aether flowing across a spherical surface representing one radial distance cannot flow across a similar surface representing a lesser radial distance, unless the velocity of the aether increases in proportion to (1/r)², with r as the spherical radius, since a spherical surface area is proportional to the square of its radius. The volume of flow per second will be the spherical surface area multiplied by the flow velocity, v, as follows:

Flow volume = 4πr²v

If the velocity at any radius is proportional to (1/r)², we will have:

Flow volume = 4πr²K/r² = 4πK

with K some constant. The velocity of the inflowing aether, however, as we know, is determined by the Newtonian escape velocity, which is proportional to (1/r)^1/2. Thus, we will have the flow volume per unit time:

4πr²v = 4πr²(2GM/r)^1/2 = 4π(2GM)^1/2r^3/2

This means that the flow volume must decrease with decreasing radius, which leaves an excess volume of aether accumulating at each radial distance throughout the field. Clearly there must be some mechanism to dispose of this excess.

There are two possible mechanisms that might be used to solve this problem.

The first is that there are two aether flows within the field, one inwards towards the centre, and the other outwards, with the outward flow serving the purpose of disposing of the accumulation of excess aether. Such outward flows would have to be constructed of

very narrow streams of aether, compared to the width of the inward flows, and therefore at a much higher velocity, perhaps faster than light, in order that the outward flow might have a negligible effect compared to the inwardly flowing aether.

The second option involves using an extra spatial dimension to dispose of the accumulating aether so that the excess inflowing aether crosses into a thin slice of three dimensional space, in parallel to the original, along this extra dimensional direction, in which it flows outwards again towards outer space. Since all massive bodies are only within the space in which the aether is flowing inwards, the outward flowing aether, in a separate space, has no influence on any of the massive bodies in the other space.

Since the second option is simpler and more effective, and lacks the problems of the first option, I will adopt a postulate that the outward aether flow occurs in a separate three-dimensional or, rather, as argued before, six-dimensional space to that of the inward flow.

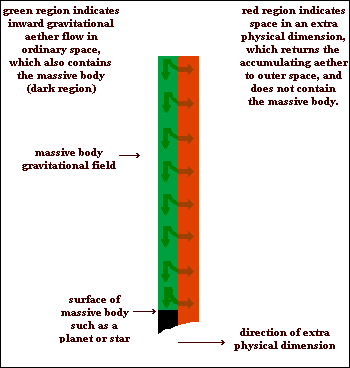
HOW IS THE INFLOWING AETHER ULTIMATELY DISPOSED OF?

The explanation given for the basis of the effect of a gravitational field on the time dilation of a clock held stationary within it, can be successfully used to immediately write down the Schwarzschild Solution for a test object in orbit around the source of a gravitational field, without any reference to the Gravitational Equations of General Relativity at all. It will be possible to obtain this equation as simply a special relativistic correction to a trajectory obtained from the force field picture of ordinary Newtonian gravitation.

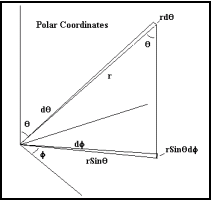
The Schwarzschild Equation, in fact, has the form of a modified Minkowski time dilation equation, so we can start by writing down this Minkowski time dilation equation, in flat space polar coordinates, for a test object moving along an orbital trajectory in the field. This is usually regarded as a metric equation, but I refer to it as a time dilation equation, since I do not suscribe to the metric interpretation. This does not matter to the equation itself, since it simply relates the same parameters, with the same values, in the same way, in either case. The initial equation, in the usual polar coordinates, is as follows:

(c.dτ)² = (c.dt)² - (r.dθ)² - (r.sinθ.dφ)² - (dr)²

where t is the time, r has the significance of a radial distance towards the centre of the field, and θ and φ are angular measures.

This is a time dilation equation, relating dt and dτ, caused by the orbital velocity, which can be obtained by dividing the spatial parameters by dt. This gives the orbital velocity of the test object in a reference frame in which the central massive body is stationary.

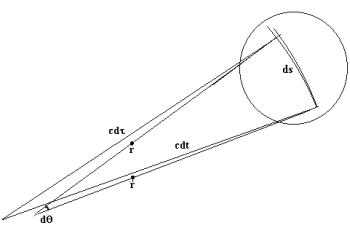
The above figure provides a rough or crude illustration of the basis of this equation for light oscillating within an orbiting clock. A more detailed, magnified version of the circled part of the diagram is given in another illustration further on. The distances cdτ and cdt represent the summation of an immense number of back and forth oscillations of light within an orbiting clock during its orbital movement through the distance ds. Since this latter movement is at a small orbital velocity, the total distance moved by light in the moving and stationary frames will be enormously larger, as is represented by the very large distances cdτ in the moving frame and cdt in the stationary frame. This is a normal special relativistic situation for light moving orthogonally to a direction of inertial motion of an object, clock, etc. The movement of the orbiting clock over the small orbital segment, ds, is assumed to be approximately equivalent to inertial motion independently of a gravitational field. The following diagram illustrates the ordinary inertial case, in which light is oscillating back and forth along a rod, R, in a direction orthogonal to the direction of inertial velocity, v, indicated by vdt. The relationships between vdt, cdt, and cdτ give the equivalent inertial minkowski time dilation equation to that mentioned above. The dotted portion shows that the back and forth oscillation can be summed to give the same equation simply multiplied by 2.

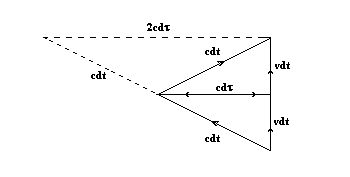
Since, however, the object we shall be dealing with is orbiting within a gravitational field, the equation is written in polar coordinates, as in the following illustrations:

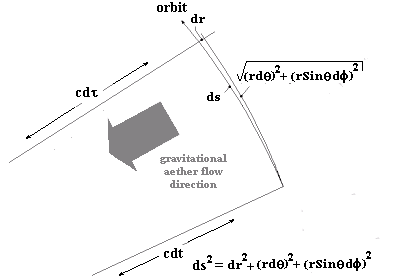
Here we have, consistent with the explanation of gravitational time dilation given before, the orbiting object moving through an aether flow that is moving inward towards the centre of the field at a specified velocity. There are three important considerations that must be kept in mind here:

1) The orbital segment, ds, is small enough to be considered to approximate a straight line, which justifies the use of the Minkowski equation, which is essentially a Pythagorean relationship.

2) The orbit is considered to be elliptical, but to depart from a circular orbit by only a very small amount, which means that dr will be very small. This also means that the inflowing aether direction can be taken to be approximately at right angles to the orbital trajectory.

3) There are thus two velocities of the orbiting object at right angles to one another - the ordinary orbital velocity and the velocity relative to the inflowing aether. An important consideration is that it will not be necessary to consider a relativistic addition of these velocities, since both velocities will be considered and examined independently, with a resultant velocity being irrelevant for the current argument. However, it will be necessary to consider the relativistic interaction of the inflowing aether velocity and the radial component of the orbital velocity (along dr), which an external space observer (outside the gravitational field) will see as being in the same direction as one another, and not independently observable.

The inflowing aether will produce added time dilation and length contraction effects, distinct from those associated with the orbital motion, and created by the inwardly moving aether, with a distinct value of γ, which I will call γ_g, to distinguish it from the value of γ associated with the orbital motion.

We may regard the inflowing aether as creating a situation equivalent to the whole orbital segment, ds, and its associated components, as illustrated, moving radially outwards at right angled to the direction of

orbital motion, with the difference that this has no affect on the magnitude of the radial distance involved. This creates the equivalent of the orbiting object moving at a velocity relative to the outer space 'stationary' frame mentioned before. We must remember that, as postulated before, all light travelling in this outer space frame behaves as light in a stationary frame, since the 'proper' light, normally intrinsic to the object, travels within the moving aether. If this were not so, the moving aether would be irrelevant for this discussion.

The oscillating light, represented by cdt, is now oscillating in the direction of relative motion between the orbiting object and the moving aether, in the manner of light in a stationary frame, as far as the outer space observer is concerned.

The Minkowski equation can also be used to obtain a time dilation equation for motion of this kind, just as for light moving orthogonally to the direction of relative motion, although it is less easy to see diagramatically, as shown below for the case involving ordinary inertial frames:

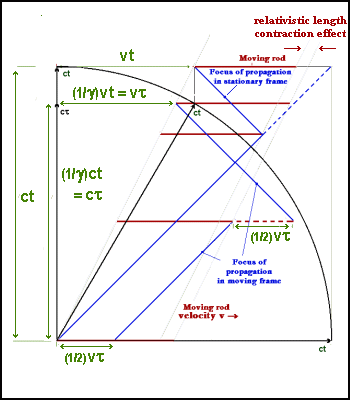
For the orbital case, the Minkowski equation can be written for ct, cτ', and dR, where dR represents the distance travelled by the moving aether relative to the orbiting object, as follows:

(cdτ')² = (cdt)² - dR²
= (cdt)²(1- (v_ae/c)²)
= (1/γ_g)²(cdt)²

This additional effect will cause the value of dt to be gravitationally time dilated to (1/γ_g)dt. That is, the clock mechanism, or time within the field, is physically modified by this factor in accordance with its elevation within the field. This, of course, is identical to the gravitational time dilation effect described in a previous section.

We thus have the working together of two separately caused time dilation effects. Both of these must be incorporated into the original orbital Minkowski equation. This can be done by simply replacing cdt in the original equation with (1/γ_g)cdt, to give

(c.dτ)²
= [(1/γ_g)(cdt)]² - (r.dθ)² - (r.sinθ.dφ)² - dr²

We must now consider the matter of the radial component, dr, of the orbital interval, ds.

In ordinary Newtonian gravitation, the orbiting object is moving at orbital speed components that are specified relative to the outer space reference frame, which is not in motion relative to the large source of the gravitational field. In the orbital motion in this frame, for an orbit that is close to circular, the components of ds orthogonal to the inflowing aether are an expression of the momentum of the orbiting object, whereas the radial component, dr, expresses the acceleration of the orbiting object, by the gravitational field, towards the central source of the field. This will cause a quantised transfer of gravitational energy, as mentioned before, to the orbiting object, by means of gravitons, the bosons of the gravitational field. If these are massless lightspeed bosons, we may suppose that they obey the principles of SR in the same way as photons.

In the case of the acceleration of a moving object via photons, the object can be seen as transferred, in a stepwise fashion, from an inertial frame at one velocity, to another inertial frame at a higher or lower velocity, depending on whether we are dealing with acceleration or deceleration. The increase or decrease of distance travelled in this new inertial frame can be regarded as a distance measured in the previous moving frame, from the perspective of the stationary frame in which the acceleration or deceleration is occurring. Since, as we know, a distance measured in a moving frame appears length contracted in a stationary frame, there is a length contraction effect across the frames during the process of acceleration or deceleration.

In the case of the gravitational field, the inflowing aether is causing the acceleration of the orbiting object through the radial distance, dr, so that we may regard a reference frame co-moving with the inflowing aether as the source of the gravitons that cause the acceleration of the orbiting object along dr. This means, however, that dr, in this frame, is length contracted compared to the length of dr in the outer space frame in which the orbit is being observed. In this latter frame, therefore, dr will be larger by a factor of γ_g. This means that we will have to replace dr, in the equation, by γ_gdr.

We know that light from the orbiting object climbs up to the outer space observer against the gravitational field, i.e., against the inflowing aether, and loses energy, becoming red shifted, so it travels withing the inflowing aether, or, in other words, relative to a co-moving aether frame. The outer space observer thus observes the value of dr in the original co-moving aether frame, and not in his own frame, although the actual value of dr in his own frame, which he cannot see directly, is really γ_gdr.

This effect does not apply to the measurement of the other components of ds, which are at right angles to the moving aether, since the length contraction effect of a length within a moving frame occurs only in the direction of relative motion. So the final orbital time dilation equation must be:

(c.dτ)²
= [(1/γ_g)(cdt)]² - (r.dθ)² - (r.sinθ.dφ)² - (γ_gdr)²

The value of the gravitational, or aether motion, factor γ_g is determined by the orbit level escape velocity, and is (1/(1 - 2GM/rc²)^1/2, and so the final Minkowski orbital equation is

(c.dτ)²
= (1-2GM/rc²)(cdt)²-(r.dθ)²-(r.sinθ.dφ)²-(dr)²/(1-2GM/rc²)

which is the standard Schwarzschild solution for the orbiting test object, as normally obtained from Einstein's gravitational equations.

One may wonder why the radial value of r, in terms like r.dθ is not a gravitationally length contracted value. The answer must be, of course, that whole parameter r.dθ is not gravitationally length contracted, being at right angles to the aether flow. This means that if we did specify r to be length contracted, we would automatically have to alter dθ to compensate, in order to keep the parameter as a whole the same. So it is not necessary to complicate the equation by examining whether or not r should be considered to be length contracted in any particular frame.

OBTAINING THE SCHWARZSCHILD EQUATION:

I shall now consider the case of a small test object free falling radially, from outside the gravitational field, directly into a black hole.

The relevant time dilation equation, in polar coordinates, will have a radial spatial coordinate only, and no angular coordinates. The equation will therefore be:

(c.dτ)² = [(1/γ_g)(cdt)]² - (γ_gdr)²

Since, however, the infalling object always keeps pace with the inflowing aether, since both are always at the Newtonian escape velocity at each radial distance, there is no relative motion between the object and the inflowing aether. This will mean that γ_g = 1, and the equation becomes

(c.dτ))² = (cdt)² - dr²

However, when the infalling object reaches the so-called black hole event horizon, the Newtonian escape velocity reaches the velocity of light. The infalling object will also reach the velocity of light and, according to this model, go beyond it after crossing the event horizon. The concept of crossing the event horizon, in this model, thus has a severe problem that must be examined, as follows:

Firstly, acceleration of the infalling object must be dependent in some way on bosonic interaction between the infalling object and the massive body aether flow. Assuming gravitons are the massless bosons involved, they will also obey the speed of light limiting velocity, so that the infalling object cannot be accelerated to or beyond the speed of light. A Newtonian escape velocity at or beyond the speed of light thus becomes meaningless, so that the speed of the aether flow at or beyond the event horizon has no basis, in this model, for any particular definition. Thus, the definition of a gravitational field effect becomes meaningless once the event horizon has been reached.

It might, perhaps, be possible to create an alternative principle for the aether flow beyond the speed of light, but two separate theories for the same aether flow does not seem satisfactory.

One way to overcome this difficulty would be if the region beyond the black hole event horizon were excluded from the gravitational field concept altogether. This would make the need for a faster than light region for the aether flow to be redundant.

Exclusion of the region beyond the black hole event horizon can be achieved if the inflowing aether simply transfers to the space that takes the aether flow back out of the field, thus taking the entire remaining aether flow back out of the field.

This, however, leaves a problem as to what to do with the space within the event horizon, which would now have a zero gravitational field, and any infalling object that might cross the event horizon, a result that is hardly satisfactory. A possible alternative is that a reversed aether flow occurs within the event horizon, which would create an anti-gravity field that would prevent an infalling object continuing to fall inwards.

Such an encounter with an event horizon aether flow

reversal, by an infalling object, would mean a very sharp reversal of gravitation, if the reversed aether flow will be also travelling at the velocity of light near the event horizon. This must virtually immediately return the infalling object to the event horizon, and the result will necessarily be that the object oscillates radially about the event horizon. This, however, will cause collisions if other objects have previously fallen into the black hole, which will dissipate the kinetic energy of the infalling object as heat. It will then eventually settle permanently on the black hole event horizon.

Thus, all the matter of a black hole becomes distributed around its event horizon. In this model, therefore, nothing can penetrate into the interior of a black hole.

This model of a black hole event horizon does not affect the normal features of a black hole. Light, for example, or anything else that reaches the event horizon, still cannot escape back to outer space.

Such a model means, in effect, that the event horizon of a black hole is a 'solid' surface, which is based on a reversal of gravity at the event horizon, and not on the normal electromagnetic field based 'solidity' of a surface. Also, the speed of the inflowing aether never goes beyond the speed of light, which is consistent with the principle of light as a limiting speed. It flows at the speed of light just at, and just below, the event horizon, thus keeping all material on the event horizon, centered on the junction between the two aether flow directions where, of course, the opposing gravitational fields would produce a resultant field of zero.

One might argue that this wouldn't work on the basis of the well known result that any gravitational field inside a mass uniformly distributed around a spherical surface would be everywhere zero. This would be the case, however, only if the field penetrates throughout the interior region within the spherical surface. If the field were everywhere restricted to a limited region just below the surface, this conclusion would not apply.

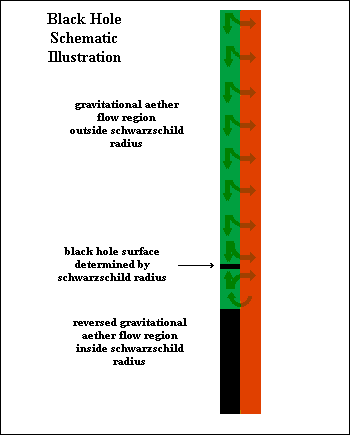
BLACK HOLES:

What I have said here does not imply, of course, any invalidation of General Relativity, although I would have a different theoretical understanding of the nature of General Relativity, as I have of Special Relativity.

On another page, in the section entitled "The Force Field Picture and the Manifold Picture", I made the case that all interactions have two fundamental viewpoints, from which they can be understood. The first fundamental viewpoint is the force field picture, which uses the concept of a force field to generate a mathematical description of the resulting trajectory of an accelerated object in a force field. The second fundamental picture considers the geometrical properties of such a trajectory, which will be curved in spacetime, by regarding it as a geodesic of some manifold (which is always possible).

What I have presented here makes use of the first fundamental viewpoint, whereas General Relativity uses the second. The problem, as I see it, with General Relativity is that it makes the second viewpoint the only possible or valid viewpoint, as if the force field picture were not only outdated, but simply wrong.

It is possible to analyse an interaction entirely from the geometrical viewpoint, but it is far more

complicated and difficult than using the force field viewpoint. What Einstein did in this regard, in the case of gravitation, was to construct a stress-energy tensor, instead of a simple accelerating force, and mathematically relate it to a geometrical curvature tensor, on the basis that the energy tensor was able to be seen as the cause of the curvature of the trajectory or, rather, the manifold of which it is a geodesic.

It should not seem strange if both kinds of analysis can produce the same result, except that Einstein gave the impression that the geometrical picture of what he regarded as the curvature of space is the only way in which gravity can be analysed. I believe, however, that this concept arises from an exaggerated importance given to the peculiarity of gravitational force, in which the applied force and the inertial response, unlike with other forces, like the electrical force, have the same factor (the mass, m) on both sides of the force field equation, which cancels out, leaving the result that all bodies, if sufficiently localised, of whatever mass, undergo equal accelerations in a gravitational field. I do not accept the argument that this should lead to the conclusion that space itself should be considered to be curved, and that a force field picture, as an alternative analytical approach, can no longer exist.

SOME REMARKS ON GENERAL RELATIVITY:

© Alen, March 2007; update Dec 2010
June 2019 - re-engineered to properly display on Chrome and Firefox.
alen.1@bigpond.com

Material on this page may be reproduced
for personal use only.