SPECIAL RELATIVITY AS A THEORY OF LIGHT
RATHER THAN SPACETIME

Summary:
The purpose of this page is to examine an alternative SR model with the capacity to account for the light postulate, the phenomenon of relativity of simultaneity, and other SR phenomena. This alternative was not examined, or even mentioned, by Einstein in his original 1905 paper, or by anyone since. The proposed model attributes SR phenomena to an undiscovered property associated with light itself, rather than to a peculiarity in the nature of the underlying spacetime. The result is a version of SR consistent with the transformation equations and established experimental results. It identifies a Galilean spacetime with Lorentzian, and not Galilean, interactions. It at least hints, in addition, at a possible basis for modern experiments with light, involving nonlocality and which path erasure phenomena, and may also be able to support a better explanation for the existence of superluminal quasar jets, which cannot at present be adequately explained.

In his 1905 paper, On the Electrodynamics of Moving Bodies, in section 2 (On the Relativity of Lengths and Times), Einstein uses the light postulate to show that moving clocks, synchronised according to a stationary system, do not appear to be synchronised according to an observer moving with the moving system.

The initial method which he uses to show the existence of the nonsimultaneity referred to, is based on the result of sending a light ray along a moving rod, reflecting it off the end of the rod, and returning it again to the start of the rod, subject to the requirement of the light postulate, which declares that light travels at a speed independent of the speed of the source which emits it. The consequence of this is that the light travels at the same speed, c, both within the moving system and also within the stationary system, despite the relative motion of the two systems. The peculiar result of all this is best understood if one imagines two pulses of light to be sent in opposite directions along the rod, from the centre to both ends.

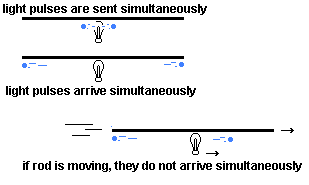
Within the moving system the rod is at rest, and the light travels at velocity c in both directions, so the light pulses will arrive simultaneously at the ends of the rod. Since, however, according to the light postulate, the light must travel at velocity, c, in both directions, in the stationary system also, it will take longer for the light pulse travelling in the same direction as the relative motion to reach the end of the rod than the light pulse travelling against the relative motion. This is because the light travelling with the relative motion is trying to catch up with the end of the rod that is moving away from it, whereas the pulse travelling against the relative motion has its end of the rod coming to meet it. This means that, while the arrivals of the pulses at the ends of the rod are both simultaneous in the moving system, they cannot be simultaneous in the stationary system.

Einstein says, in his paper:

"So we see that we cannot attach any absolute signification to the concept of simultaneity, but that two events which, viewed from a system of co-ordinates, are simultaneous, can no longer be looked upon as simultaneous events when envisaged from a system which is in motion relatively to that system."

(Note that, here, Einstein refers to 'events' as single objects common to different systems of coordinates. He does not refer to the possibility that an event in one system of coordinates might not be the same event in another system of coordinates. He has, in effect, already assumed that the transformation equations, which he will

derive, are to be considered as simply coordinate transformations, without any consideration of the possibility they could be transformations of any other kind.)

The contradiction in respect of simultaneity, of course, is contrary to normal expectations, and this is because the light postulate, that declares light to travel at the same velocity in both systems at the same time, is itself contrary to normal expectations. This situation must therefore be given some rational explanation, if the light postulate that gives rise to it is to have any credibility.

There are, therefore, three questions that arise. Einstein, however, appears to have never clearly distinguished these three possibilities, or subjected them to a full examination, but simply assumed that an affirmative answer to only one of them (no 2 below) was the correct answer.

Since the argument about nonsimultaneity is determined by a situation involving the use of both light and spacetime, and not either alone, the following are the three questions that must arise:

1) Is the conclusion of nonsimultaneity, and the working of the light postulate, an appearance caused solely by the working of the light itself, in accordance with the light postulate, and not by any other cause that exists independently of the light?

2) Is the conclusion of nonsimultaneity, and the working of the light postulate, an appearance caused by some underlying property of space and time themselves, in the context of the relative velocity of inertial frames, that the working of the light only reveals, but doesn't actually cause?

3) Is the conclusion of nonsimultaneity an appearance caused by a combination of both of the above suggested possibilities?

These three questions have never been properly examined, and it has always been simply assumed that the answer to the second question is yes, to the point that the three questions appear to have never even been formulated and distinguished, by Einstein himself, or anyone else.

It would seem to me that, if an affirmative answer to the second question is problematic, as I have argued elsewhere on this website that it is, an affirmative answer to the third question, involving a combination of affirmative answers to both the first and second questions, is not likely to be any less problematic. Therefore, I would say that the most important course of action is to concentrate on examining the possibility of an affirmative answer to the first question, combined with a negative answer to the second. This is not only because the matter has never yet been considered, but also because important criticisms can be made against an affirmative answer to the second question.

The historical, affirmative answer to the second question led to a new concept of the nature of space and time, which is referred to as Minkowski spacetime.

PART 1 - THREE QUESTIONS THAT EINSTEIN DID NOT CONSIDER:

Here, I shall attempt to examine what might be the result of a supposition that the correct model that should be used to interpret the paradoxical phenomenon of relativity of simultaneity involves an affirmative answer to the first question, which was:

Is the conclusion of nonsimultaneity an appearance caused solely by the working of the light itself, in accordance with the light postulate, and not by any other cause that exists independently of the light?

We do not need to examine, here, the derivation, or the mathematics, of the SR equations themselves, since we have to consider only the interpretation of the working of the light postulate and the consequent conclusions regarding nonsimultaneity effects between two relatively moving frames. Since we are to consider an alternative to the spacetime rotations concept, we must return to the original context of the dynamical derivation of the equations, in terms of the two postulates of SR, and not make any assumption that any spatial or time coordinate axis is rotated in spacetime relative to any other.

Let us, therefore, return to Einstein on his railway embankment, and consider how light appears to travel within a moving train from the perspective of both the observer on the embankment and the observer on the train. Let rays of light be emitted, at the same time, from the centre of a train carriage to both ends. For both observers, the rays of light are emitted simultaneously, since they form only a single event for either observer. As we know already, according to the light postulate, and the conclusion of nonsimultaneity, the light rays will simultaneously reach the ends of the carriage in the view of the observer on the train, whereas they will not simultaneously reach the ends of the carriage in the view of the observer on the embankment.

Such results were interpreted to indicate that time cannot be the same for both observers, which then led to the conclusion that there is no such thing as a universal, common time for all observers and, thereafter, to the concept of Minkowski spacetime. This was thus an assumption that the answer to the second question must be yes. It is a pity, I would say, that no one was there at the time to say "wait a minute - is that really the only possible explanation for the above nonsimultaneity effect?" This time, therefore, we shall attempt to examine an alternative explanation, in terms of an affirmative answer to the first of the three questions.

It might appear obvious that time cannot be the same for both observers, since both see the same light, and yet see it describing the same events nonsimultaneously. Is it not merely an assumption, however, that both observers 'see the same light'? What does this assumption actually mean?

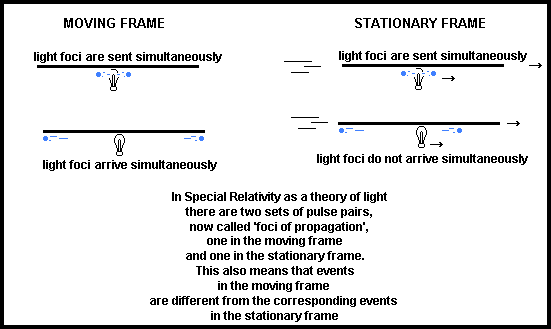
We might suppose it to be obvious that a particle of light, a photon, is a single entity, a single focus of propagation, that can be picked up by either observer. But, granted that a photon can be regarded as a single entity in itself, is it not, nevertheless, merely an assumption that it is, as it were, identical with its focus of propagation? Suppose, therefore, we postulate a distinction between a photon, as an entity, and its focus of propagation, and ask the question: could a single photon, perhaps, have more than one focus of propagation at the same time? Might the observer on the train and the observer on the embankment really not be seeing the 'same' light after all?

If, indeed, a photon has a focus of propagation in the carriage reference frame distinct from its focus of propagation in the frame of the embankment, it is then easy to consider the possibility that their individual trajectories in space and time might be distinct also. The criterion for identifying the nature of the difference between the trajectories of the two foci of propagation will then be simply the light postulate. That is, a photon will have a focus of propagation travelling at velocity c in the carriage reference frame, and a different focus of propagation travelling at velocity c in the embankment reference frame.

Such a condition can fully account for the nonsimultaneity effect in the observation of the same event by the two different observers. That is, the observer on the train encounters a photon by means of a different focus of propagation, at a different time, than that by which the observer on the embankment would encounter the same photon. Thus, the implication that time, itself, is not the same for both observers no longer exists. The explanation, instead, is that it is light, and not time, that is not the same for both observers and, in general, for different inertial observers in relative motion.

The consequence of this is then that, as the foci of propagation in the two frames are distinct from one another, they also create distinct events in the two frames. That is, the focus of propagation that strikes the right hand end of the carriage in the moving frame creates a spacetime event that is distinct from the spacetime event at which the stationary frame focus of propagation appears to strike the right hand end of the carriage in the stationary frame.

The Lorentz transformation equations will thus be no longer simple coordinate transformations of a single event from one frame to another; instead they must become a kind of one-to-one mapping of the coordinates of an event in one frame to corresponding coordinates of a different event in the other.

PART 2 - AN ALTERNATIVE INTERPRETATION
OF THE LIGHT POSTULATE (1):

A proposal that photons have different foci of propagation in moving and stationary frames creates immediate implications regarding the intrinsic nature of such photons that must be considered. There is obviously nothing special about the two reference frames in the example above, so that, if a photon has two distinct foci of propagation in the two frames, it must be supposed to have distinct foci of propagation in all possible inertial reference frames at all possible relative velocities less than the velocity of light. In other words, it must have an entire spectrum of foci of propagation, together with an entire spectrum of trajectories associated with such foci of propagation. If, despite this, the photon is to remain as a single entity, that can still be regarded as a single photon, all these foci of propagation, and their trajectories, must necessarily be connected together in such a way that, together, they can constitute a single entity.

I suggest that the easiest way in which this might be thought possible is to postulate that they all form part of a single geometry of the photon in space and time. That is, a photon will be considered to project, into space and time, a geometry of some material kind, belonging to, or internal to, itself, within which all its foci of propagation, and their trajectories, will be defined, determined, and connected together to form a single reality.

In such a scenario, it is important to try to clearly understand what might be meant by a 'focus of propagation'. Does it mean, for example, that a photon occupies many different locations at the same time? I would say that the answer to that would have to be in the negative, in order to avoid possible paradoxical misconceptions of the reality involved. Instead, it would be more satisfactory to suppose that the foci of propagation of the photon are merely features of the photon's own spacetime geometry, that define the locations at which, alone, the photon is able to be detected. If, then, a particular focus of propagation is selected for the detection of the photon, the photon will manifest at that location with, at the same time, the withdrawal of its entire, internal spacetime geometry, along with all the other foci of propagation, and their defined trajectories. It will be necessary, however, to distinguish between a photon reflection event, at which it is not absorbed, and an event at which it is absorbed, or detected, by a target.

Note that, for all this to work, the photon will have to somehow 'know' which of its foci of propagation is approaching any target at velocity c. This is the means by which the photon can be enabled to distinguish between one inertial frame and another. This may seem strange but, I think, no more strange than the fact that, in modern which-path erasure experiments, it has been found that the photon seems to 'know' that which-path information has been erased, even after it has passed the section of the experiment which determines whether which-path information can exist or not.

It is worth remarking, here, that, in this explanation, there is no spacetime rotation of inertial frames, and space and time axes remain parallel, as they were always thought to do in the former Galilean era. Thus, all the problems that arise in connection with such axial rotations are swept aside.

The above proposal regarding the nature of light is strengthened by an added benefit automatically associated with the concept of such a suggested internal spacetime geometry of photons (not as a Minkowski type geometry, by the way). Such a proposal involves a projection of the

internal geometry of a photon into space and time at a speed so great that the nature of the photon becomes effectively 'nonlocal' in its conception. Such a speed of projection of the photon's internal geometry does not, by the way, violate the principle of the propagation velocity of light, c, as the maximum possible. Within such a geometry, the photon can appear only at the location of one of its foci of propagation, which propagate, within the photon's geometry, only at velocity c.

The purpose of projecting such a geometry into space and time at such a speed is to enable the creation and calculation of the entire spectrum of trajectories of all the foci of propagation, which they will then follow, at their normal propagation velocity.

Such an internal geometry, attributed to the photon, can thus easily also form the basis of an explanation of the working of photon non-locality, which-path erasure, and entanglement, as seen in a variety of recent experiments. In other words, the geometry projected into space and time by a photon will be withdrawn, or will 'collapse' when the photon reaches its destination, where it is detected.

Entanglement, for example, in this view, would require only the proposition that two photons are sharing a common spacetime geometry, rather than having separate geometries, in the usual way. Then, the detection of one photon, with a withdrawal of its internal geometry, would automatically withdraw the internal geometry of the other photon also, thus necessitating it be also detected virtually simultaneously with the first, however far apart they might be.

Again, in a which-path erasure experiment, it can easily be conceived that, since the photon does not appear until one of its foci of propagation is selected, it is quite possible that it could virtually instantaneously modify and 'recalculate' its internal geometry, past, present, and future, in response to any modification of its environment, at any time up to the point where it actually reaches its target, even if its foci of propagation have already passed the double-slit part of an experiment, or its equivalent.

If it turns out that the above explanation is the correct interpretation of SR, then we will have arrived at the end of the Minkowski spacetime era, and Minkowski spacetime will have been revealed as one of the great conceptual errors in the history of science.

The new reality, if established, will involve a restoration of the former Galilean spacetime with, however, a preservation of the Lorentz transformation equations. This implies that interactions in this spacetime, as mediated by lightspeed bosons, are Lorentzian in nature, and not Galilean. The transformation equations, as mentioned already, will no longer be simple geometrical coordinate transformations but, rather, a special one-to-one mapping of events, as observed in one frame, onto those as observed in another. Along with the restoration of Galilean spacetime, we will also have the restoration of a common, universal time for all observers, with the difference that, due to the working of light, it will not be directly visible across all inertial frames to all observers. I have already argued this on a page dealing with the twins paradox.

As mentioned here, it may also provide a single, unified theory that will underlie both SR and all nonlocality effects, as observed in recent experiments.

PART 3 - AN ALTERNATIVE INTERPRETATION
OF THE LIGHT POSTULATE (2):

PART 4 - ILLUSTRATIONS:

One might argue that it seems peculiar that the quadratic nature of the equation that gave rise to the Minkowski spacetime interpretation exists, if no such spacetime exists. However, the source of the quadratic nature of the equation can easily be seen in terms of the movement of a light ray transverse to the direction of relative motion, in accordance with the light postulate.

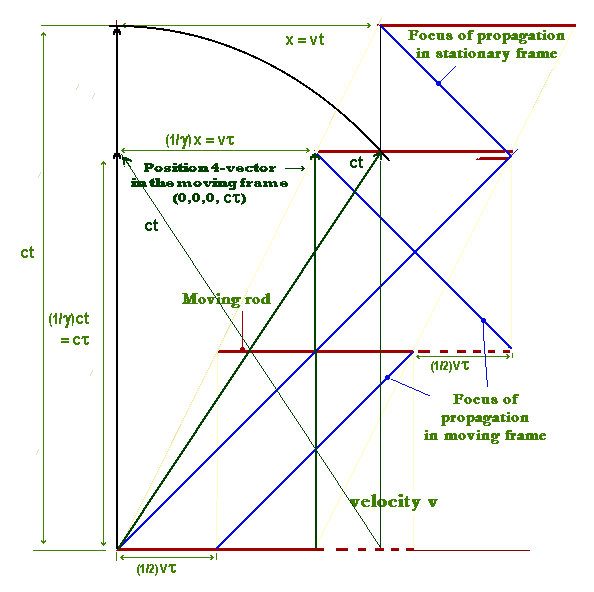
In the stationary frame, the focus of propagation moves along a hypotenuse, ct, the moving frame moves a distance, vt, in the direction of motion, and the focus of propagation of the light moves at right angles to the direction of motion in the moving frame, (ct), thus creating a right triangle, which immediately gives the equation that forms the basis for Minkowski spacetime, as

(ct)² = (ct)² - (vt)² = (ct)² - x² - y² - z².

This can be seen in the right triangle made by ct and vt in the diagram on the right.

THE MINKOWSKI EQUATION:

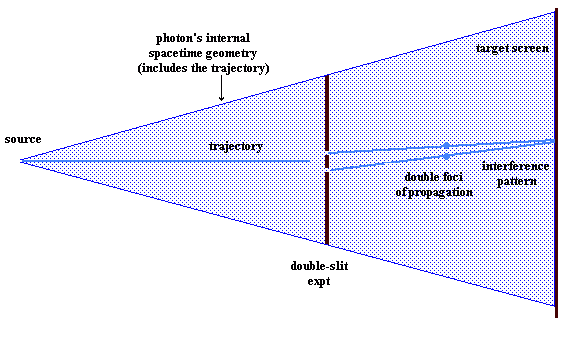
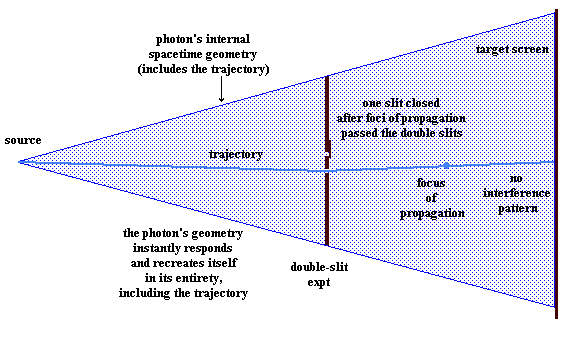
WHICH PATH ERASURE EXPERIMENTS:

The above illustrations suggest how the concept of an internal spacetime geometry of a photon might help to explain the working of which-path erasure experiments and the like. I do not attempt to explain how the foci of propagation tie in with the wave theory of light. That is a problem that exists in any case.

In the left illustration, a double focus of propagation, within the same frame, is used to roughly indicate a splitting of the focus of propagation by the double slit experiment. This concept is sufficient for present purposes.

The essential value of these illustrations is in the concept of the projection of an internal spacetime geometry of the photon, indicated by the shaded areas, being projected instantaneously into spacetime, within which the trajectory of the photon from source to target is established, independently of the actual propagation of the photon. The focus, or foci, of propagation then determine the location along the trajectory at which the photon can be detected at any particular time.

The photon itself is identified with its spacetime

geometry, and not merely with its foci of propagation. When a focus of propagation strikes the target, the entire spactime geometry collapses onto that location, and a photon appears there.

Any relevant environmental change, affecting the photon's geometry, will create an instantaneous response by the photon, throughout its entire geometry, which will be retransmitted, instantaneously, from source to target, and will include, if necessary, a new trajectory. This will be independent of where the focus of propagation currently happens to be, and the focus of propagation will appear on the new trajectory, at the appropriate position.

This could potentially serve to explain how the interference pattern on the target screen can be made to disappear, even after the focus, or foci, of propagation have already passed the slits themselves. In a similar manner, the interference pattern can be restored again by opening the slit which has been closed, before the focus of propagation strikes the target. This thus erases the which-path information that previously existed after closing one of the slits.

ILLUSTRATION OF PHOTON MULTIPLE FOCI OF PROPAGATION:

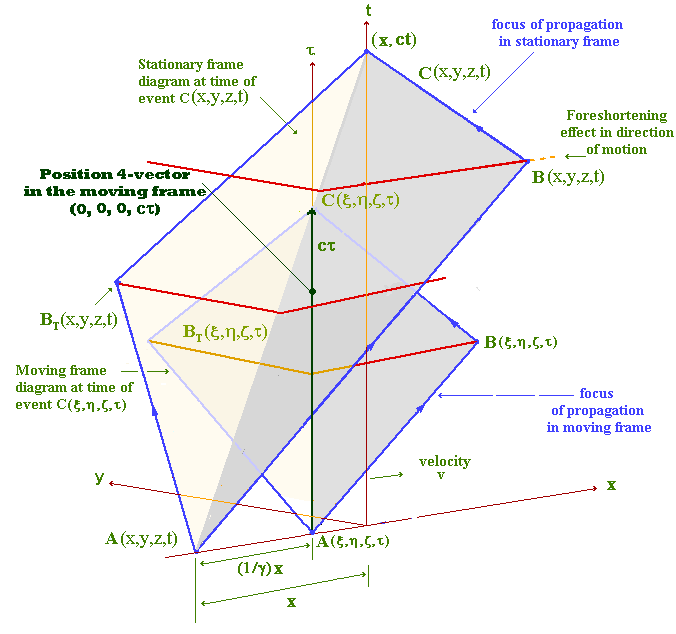
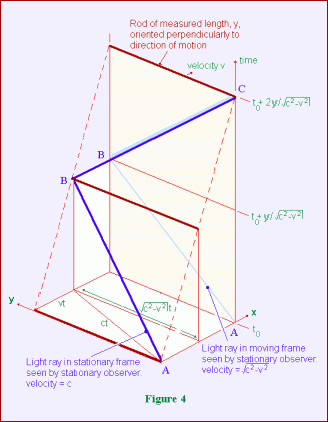
The illustration shows two rods, at right angles to one another, lying along the x and y directions, and moving at velocity, v, in a stationary frame along the positive x direction. The blue rays show a lateral pulse of light reflected off the end of the rod in the y direction, AB_tC, and another pulse reflected off the end of the rod in the x direction, ABC.

There are two diagrams, which show separate foci of propagation of light: in the moving frame (the blue lines in the smaller diagram), and in the stationary frame (the blue lines in the larger diagram).

In the smaller diagram, the blue lines are symmetrical in the x and y directions, since they are in the moving frame, and unaffected by the relative motion. In the larger diagram, the blue lines are not symmetrical, being affected by the relative motion, and the reflection off the end of the rod at B involves an apparent foreshortening of the length of the rod in the x direction.

The blue lines, laterally and in the direction of motion, coincide at C in both diagrams. That is, the relative motion does not cause the frequency of oscillation of light to differ along the x or y axes, in the stationary frame diagram. This would not be the case, in the stationary frame, if there were no length contraction effect produced by the focus of propagation in the stationary frame.

Since spacetime here is Galilean, the spacetime coordinate systems of both diagrams are parallel to one another. That is, there is no relative rotation of coordinate axes, as is the case with Minkowski spacetime. It is assumed that light moves at velocity, c, in the direction of time, as well as in the spatial direction.

In view of this, the position of event C(x,y,z,t),

in the moving frame, with respect to the stationary frame starting event A(x,y,z,t), is at (vt, ct), or ((1/g)x, ct), as is shown more clearly in the diagram below. This event is not visible in the stationary frame, since it is visible, via the moving frame focus of propagation, only to the moving observer. In the stationary frame, this event becomes visible, via the stationary frame focus of propagation, at event C(x,y,z,t), at (vt, ct), or (x, ct), or, more accurately (x, 0, 0, ct), and this expression of the stationary frame manifestiation of a moving frame event can be used to construct the so-called spacetime interval, and the associated 4-vectors (see below).

Since event C(x,y,z,t), at time t, is a stationary frame manifestation of the moving frame event, C(x,y,z,t), at the earlier time t, a moving clock will appear time dilated. As I have argued elsewhere, this is to be interpreted as the stationary frame observer viewing a moving clock via a present view of its past history.

The reason for using events C is that they represent one complete back-and-forth oscillation of a photon, and the (x, 0, 0, ct) specification can be applied to any event C that is determined by any number of completed back-and-forth oscillations of a photon. The single back and forth oscillation of a photon shown, can thus represent the general internal oscillations of bosons within any moving object, and hence the relationship between the object as it is in the moving frame, and as it is manifested in the stationary frame.

The first diagram, below, shows two complete oscillations, corresponding to the single oscillation shown in the second diagram, below it, to indicate the existence of multiple oscillations being described in the same way mathematically, in which (2x, 0, 0, 2ct) would become (nx, 0, 0, nct)

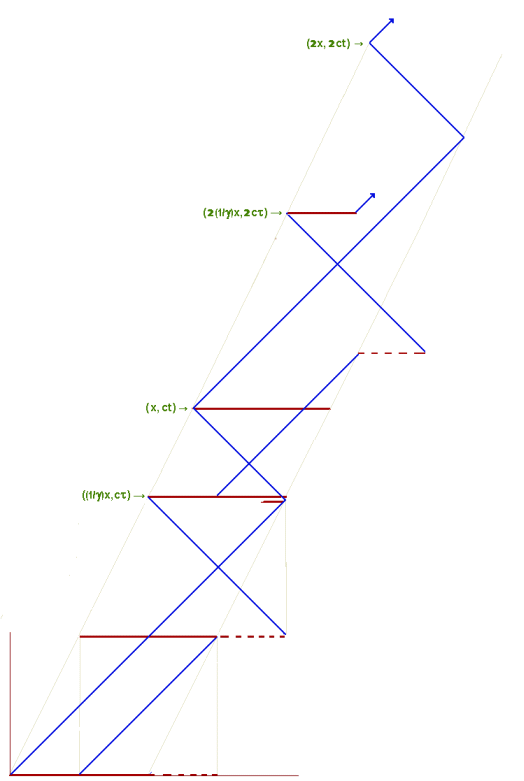
One of the problems with SR as a theory of light rather than a theory of spacetime is the consequences caused for other theories in Physics by the loss of the Minkowski metric, and Minkowski 4-vectors, in which these are used extensively.

However, on the supposition that all reference frames travel at velocity c, in a fourth dimensional direction through time, it is still possible to construct these 4-vectors. They will simply have a different interpretation, as follows:

In a spacetime view of an inertial reference frame, an object is travelling in the time direction at velocity, c. The distance travelled in this direction, in a Galilean spacetime, is ct, which is the so-called spacetime interval in Minkowski spacetime. This distance terminates in a spacetime event, which is defined by the position 4-vector within the moving frame. Dividing by the time, t will give the 4-velocity, c, and multiplying by the rest mass of the relevant object at this event will give the momentum 4-vector in this direction, m₀c. These are Lorentz invariants and, although they are not visible in a stationary frame, they can be identified via stationary frame vector components, which will be different in different stationary frames, relative to which the moving frame will have different velocities.

The position 4-vector in the moving frame connects events (0,0,0,0) and (0,0,0,ct). To set up the stationary frame vector components

requires using the second event as it appears in the stationary frame, via the stationary frame focus of propagation, at stationary frame event (x,0,0,ct). The above diagram shows how this can be used to set up the following equation, expressing the length of the position 4-vector in terms of stationary frame components:

Position 4-vector:

S₄² = c²t² = c²t² - x²

Velocity 4_vector:

V₄² = (S₄/t)² = c² = g²c² - g²v²

Momentum 4_vector:

P₄² = (m₀V₄)² = m₀²c² = m₀²g²c² - m₀²g² v²
or
m₀²c² = m₀²g²c² - p² = (E²/c²) - p²

with E as energy, from which we get:

Energy:

E² = c²p² + m₀²c⁴

with p as relativistic momentum. All this appears here, in the context of SR as a theory of light, without the existence of any Minkowski spacetime.

FOUR-VECTORS, WITHOUT MINKOWSKI SPACETIME:

PART 5 - FURTHER CONSIDERATIONS (added March 2011):

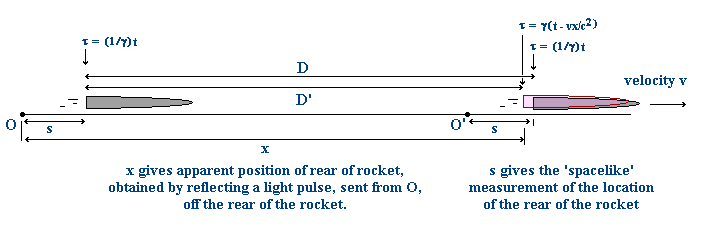
This question requires examination because of the fact that, in Special Relativity as a Theory of Light, the measurement of a moving length, in a spacelike manner, in a stationary frame, does not give the same result as a measurement obtained by sending a light ray along it. This difference is illustrated in the above diagram, in which the measurements s constitute the 'spacelike' method of locating the positions of the rockets, while the distance x, to locate the position of the right hand rocket, is obtained by sending a light pulse along this distance. (See also my page on Bell's Spaceship Paradox for an argument about this).

This means that a spacelike measurement of the

relativistic composition of velocities will also not give the same as the usual result, in accordance with the transformation equations. That is, from a spacelike perspective, a moving object, accelerated within the moving frame, will be further ahead of where it would be according to the usual composition of velocities equation. This corresponds to the distance D, in the illustration, being greater than the distance D'.

The question is, would this provide for a spacelike based composition of velocities to allow an object to be accelerated to faster than light velocities? The diagram below will help to answer this question

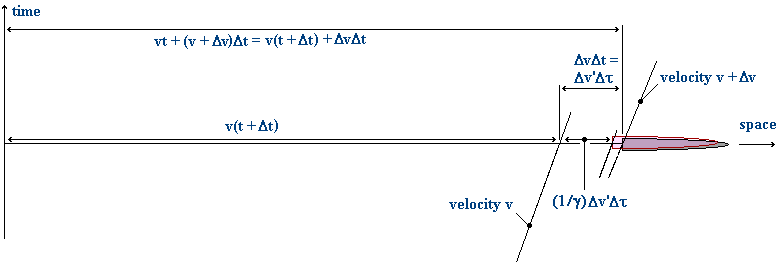
We will examine an accelerating rocket in terms of a stepwise transfer from an inertial frame at a lower velocity to an inertial frame at a slightly higher velocity. In the above diagram the rocket speed increases, in a single step, from v to v + Dv, in the stationary frame, still in the original direction.

In the stationary frame, the rocket has been travelling at velocity v, which means that the rocket is in a moving frame travelling at this velocity. The rocket instantly increases velocity to v + Dv. It is now in a second moving frame, at velocity Dv', measured within the first moving frame. It has travelled a distance DvDt, as measured in the stationary frame, in this second moving frame, in stationary frame time Dt.

We have to find the relationship between this distance, measured in the stationary frame, and this distance, measured in the first moving frame. This is the same problem as measuring the length of a moving rod, except that the 'moving rod' is now a distance created at a velocity, Dv', in a moving frame. This is similar to a case where the moving rod is changing its length as it moves. That is, we might have a moving rod, AB, in which the end B is moving at some velocity relative to A within the first moving frame (i.e., B's motion constitutes a second moving frame).

The current example would correspond to such a moving rod, in which the initial length is zero. This means that finding this 'moving rod' length will enable us to find a relationship between the velocity Dv', within the first moving frame, and its value, Dv, as seen in the stationary frame. If there can be a simple addition of velocities, v + Dv', in the stationary frame, (i.e. if Dv' = Dv), then faster than light travel is possible.

This, of course, is a matter of the spacelike measurement of the velocity in the stationary frame, as mentioned already (i.e. position measurements based on s, not x, in the initial illustration). The current illustration shows two positions for the rear end of the rocket, which is used to calculate velocities. The position slightly to the left indicates the length contraction of the distance, as specified by the transformation equations. The position to the right is the spacelike determined position of the rocket.

The distance, as given by the transformation equations, is:

x = g(x - vt)
or
(1/g)x = (x - vt)

(1/g)x is a length contracted distance, so that the non_length_contracted distance, in the stationary frame, representing a spacelike measurement of the distance, is simply x, which is also Dv'Dt. So we have:

x = Dv'Dt = DvDt

and, since Dt = (1/g)Dt (see first illustration above), we have:

(1/g)Dv' = Dv

Since, however

(1/g) = (1 - (v/c)²)^1/2

approaches zero as v approaches c, we thus have the possible result that Dv approaches zero as v approaches c, which would mean that faster than light velocities would be impossible to achieve.

One has to be careful, however, in interpreting this equation, since this result is due to a time dilation effect only, without the involvement of any corresponding spatial distance effect. That is, it is necessary to consider the alternative interpretation that Dv' increases, rather than Dv decreasing, with increase in v, for the following reason:

Since Dv' = x/Dt, and Dt is a time dilated value in the stationary frame, while x is a true value (in the spacelike perspective), it follows that Dv' appears larger, in the stationary frame, than it is in reality, in the moving frame. This is because Dt approaches zero, and consequently Dv' increases towards infinity, as seen from the stationary frame, as v approaches c, and the equation therefore does not mean that Dv approaches zero.

It must be remembered that, in SR as a Theory of Light, Dt is not an invariant, if it is related to the current stationary frame time, as it would be in the spacetime version of the theory, and time is the same in all frames, although it is not observed to be so. The interval Dt is perceived within the past history of the moving frame, although in terms of the present distance x. So the corresponding real time interval in the moving frame is greater than Dt

The key to the correct interpretation is, therefore, the fact that x is the same value in both frames, which really means that the true relationship between the velocities in the two frames is:

Dv' = Dv

This means that faster than light travel can actually occur, because the resultant velocity in the stationary frame (if measured in a spacelike manner) is a simple addition of velocities, v + Dv' (using the real version of Dv' within the moving frame).

It is to be noted, however, that an object cannot be accelerated to faster than light speed in a single frame only, since lightspeed bosons limit the acceleration interaction in any single frame. An object has to be accelerated within at least one moving frame in order to reach such speeds.

Two separate arguments are necessary to answer this problem.

Firstly, let us consider a theoretical object already moving faster than light. Let a rod AB be moving faster than light in the direction AB. It is clear that a photon (i.e. its focus of propagation in the stationary frame) leaving A will fall behind the rod, and can never reach B. Similarly, if a rod AB' is connected to the original rod, at right angles to the direction of motion, a photon leaving A can also never reach B'. This means that, in this context, the SR transformation equations cannot be derived, and are therefore irrelevant. That is, they cannot have any application in a faster than light context. The same argument applies at lightspeed also.

Secondly, let us more closely examine the nature of relativistic momentum. This is given as:

P_r = gm₀v

where m₀ is rest mass. In this equation g can, in fact, be applied either to the rest mass, creating relativistic mass, or to the velocity which, in our case, will prove more useful. We therefore have:

P_r = m₀gv = m₀gds/dt = m₀ds/(1/g)dt
= m₀ds/dt

In this version of the equation, v is replaced by a time dilated velocity, which approaches infinity as v approaches c. We must consider, however, that all measurable quantities must be quantised, so that velocity really does increase in a discrete, stepwise manner. This means that the time dilated velocity cannot actually become infinite, but must reach a finite maximum value, which therefore provides for a theoretical possibility that could enable a moving object to cross the light speed barrier.

The above objection, therefore, is not an absolute impediment to superluminal velocities, where these are achieved by multiple stages of acceleration in multiple moving frames. In addition, at superluminal velocities, there is no relativistic mass effect, since the subluminal relativistic mass effect can be alternatively regarded as a relativistic velocity effect.

A Note on Kinetic Energy (KE): It is possible to derive the usual approximate expression for kinetic energy from the relativistic energy form, in a way that avoids assigning g to the mass, rather than to velocity, as follows:

KE = relativistic energy - m₀c²
= (p²c² + m₀²c⁴)^1/2 - m₀c²

we can convert p²c² to a more convenient form:

p²c² = m₀²g²v²c²
= (m₀²v²c²)/(1 - v²/c²)
= m₀²c⁴(1/[c²/v² - 1])

Here we started with the form m₀²g²v²c², which allows assigning g to v rather than m₀. Adding m₀²c⁴ in the original relativistic energy expression, we get

[m₀²c⁴(1 + c²/v² -1)/(c²/v² -1)]^1/2 = m₀c²g

which gives us

KE = m₀c²(g - 1)

from which, using the usual Taylor series expansion for g, we get, finally

KE = 1/2(m₀v²)

approximately, where v << c, in the usual way.

OBJECTION: HOW CAN THIS BE POSSIBLE, IN VIEW OF THE RELATIVISTIC MASS EFFECT, WHICH WOULD SPECIFY THE NEED FOR INFINITE MOMENTUM AND KINETIC ENERGY TO ENABLE A MASSIVE OBJECT TO EVEN REACH THE SPEED OF LIGHT?:

Quasars have been observed to emit thin jets of charged particles enormous distances in both directions along a single axis. These observations have been used to calculate apparent superluminal velocities of the jets, up to numerous times the speed of light. Explanations have been proposed to suggest how such results might be possible without violating the light speed limitation that is apparently intrinsic to Special Relativity. That is, the superluminal

velocities are argued to be illusory, due to optical effects. The previous sections, however, show that, in SR as a theory of light, superluminal velocities are not forbidden. This conclusion therefore allows the possibility that such jets may indeed be travelling at superluminal velocities. There would, however, have to be multiple stages of acceleration - i.e. within, and along, the jets themselves, and not only in the reference frame of the quasar itself.

SOME REMARKS ON SUPERLUMINAL QUASAR JETS:

© Alen, March 2007; update Dec 2010.
June 2019 - re-engineered to display properly on Chrome and Firefox
alen.1@bigpond.com

Material on this page may be reproduced
for personal use only.