A FUNDAMENTAL GEODESIC PRINCIPLE
IN GEOMETRY AND PHYSICS

PART II - HAMILTON'S PRINCIPLE OF LEAST ACTION

The argument in part I was to establish the principle that the geodesics of any manifold can be regarded as immediate, and do not have to be derived. What this implies is that they must be immediately obtainable, by suitable experiments, within any real manifold, and this, in turn, implies that the geodesic is always the fundamental intrinsic property of a manifold through which real things, that are intrinsic to, and move within, the manifold, must always be related to the manifold.

Since the laws of physics in nature are dependent on a geometrical mathematics, the laws of physics must always equally display an adherence to the fundamental properties of geodesics in manifolds of all kinds. Where a reality subject to the laws of physics depends on motion along a geodesic in one manifold, it will display such motion along a geodesic in any other manifold on which it depends in a similar way.

One may enquire as to what is the justification for such a statement, and the direct answer is that there is no alternative, as the argument in Part I has demonstrated that there is no fundamental difference between the concept of a geodesic in one manifold compared to another, and every geometry, in every manifold, depends on this concept.

Indeed, an intrinsic concept of a manifold, and all its properties, itself depends on the concept of the geodesic, so that a manifold, intrinsically that is, is essentially simply the limitless set of its geodesics. This means that nature itself cannot relate objects, on an intrinsic basis, to any resultant manifold other than through its geodesics. It is possible to cite direct experiments that can demonstrate this truth.

Consider how one might find a geodesic in Euclidian space. It can be done by stretching a string taut between point A and point B. The string will then lie along the geodesic, or straight line, joining A and B. Now take a smooth, polished surface of a sphere, and take a frictionless, or at least well lubricated, string, and pull it taut between points A and B on the surface of the sphere. It will then lie along the geodesic joining A and B. Again, fire a projectile in a direction, in outer space, where the manifold is approximately Euclidian, from point A to point B, and it will follow the Euclidian geodesic, or straight line, joining A and B. Now take the polished surface of a metal bowl of hemispherical, or paraboloidal, or any other non-specific but similarly smooth form, and fire a ball bearing tangentially into the surface of the bowl, and it will always cross the bowl via a geodesic of its surface.

Note that, in this respect, I have referred only to 'resultant' manifolds, meaning those to which objects are confined. That is, if a geodesic trajectory across a curved bowl is viewed from a different manifold, such as the euclidian space, the trajectory will obviously not be a geodesic.

These examples support the assertion of the fundamental equivalence, in the laws of nature, of all geodesics of all kinds, which corresponds to the fundamental equivalence of all geodesics in their original geometrical definitions. It is thus possible to adopt the principle that all geodesics of all kinds are directly accessible by suitably chosen experiments, and this confirms that the geometrical analysis of any real manifold can begin directly with its geodesics, and those of curved manifolds thus do not have to be derived from the supposedly more fundamental Euclidian geodesics.

THE GEODESIC AS A FUNDAMENTAL PRINCIPLE IN NATURE:

Since we appear to have reduced the whole of geometry to a matter of geodesics, it may be asked: what has become of the status of non-geodesics? It would appear to be nonsensical to assert that they no longer exist. It would also appear to be manifestly wrong to say that nature never makes use of them.

Consider, for example, the hypothetical case of two strongly electrically charged bodies orbiting in a gravitational field. They will be travelling along geodesics of the manifold set up by the field. If however, they happen to pass close enough to one another for their electrical fields to influence their relative motion, they will deflect one another from their orbital paths, and both will cross to new orbital paths, which will be new geodesics of the gravitational field. It is clear, however, that the transitional paths by which they cross from one geodesic of the gravitational field to another will be non-geodesics of the gravitational field. So, clearly, nature does make use of non-geodesic paths, as well

as geodesic paths.

It must be remembered, however, that, in describing the transition paths of the objects as non-geodesics, we are describing them as viewed from the standpoint of the gravitation manifold alone. If, however, we consider the possibility of a manifold as set up jointly by the gravitational field and the electrical fields of the objects, we must, on the geodesic principle, conclude that such a manifold exists, and that the transitional paths are, in fact, geodesics of this jointly constructed, temporary, transitional manifold. That is to say, any apparent non-geodesic path in nature is such only from the perspective of a particular, arbitrary manifold, but never from the perspective of the manifold determined by all the laws of nature operating together in the particular case.

THE STATUS OF NON-GEODESICS:

The above considerations regarding geodesics necessitate further examination, because they have serious implications for the status of manifolds vis a vis the sources that cause them.

Consider, for example, a person stationary on the surface of a gravitational body. He is not in free fall, and is therefore not following the geodesics of the gravitational manifold but, on the geodesic principle, he has to be travelling, in spacetime, on the geodesic of some manifold. This non-gravitational manifold is set up as a resolution of a conflict between the gravitational manifold and the electromagnetic fields that prevent the person being in a free fall condition. We can therefore see here an important distinction

between manifolds and the sources that cause them.

The manifold that any such single source, like a gravitational body, causes can clearly be modified by the activity of another source, like an electrical body. We thus have the consequence that manifolds can be changed, while their sources, themselves, cannot. The result of this must be that it is such sources alone, and not manifolds, that must be the fundamental realities. Manifolds are consequential only, and a manifold may be determined as a resultant manifold produced by the working against one another of sources of different kinds.

THE CAUSES OF MANIFOLDS IN NATURE:

The above considerations have implications for the modern, exclusively geometrical picture of gravitation provided by General Relativity, in that they suggest the working of a force field picture as a distinct cause of the modification of manifolds and, perhaps, as fundamentally a cause of all manifolds, in a manner distinct from the manifolds themselves.

This really implies the existence of a force field picture in its own manifold, distinct from the manifold to which it gives rise, in which no forces appear to be acting. This would apply to forces of all kinds, and not only that of gravitation.

Let us take a simple example of ordinary Newtonian dynamics, as provided by the equation F = ma. This equation describes the interaction of the source of a force with an object of mass m, which gives rise to an acceleration trajectory of the object, which is curved. This force/acceleration transaction is set up in a Euclidian manifold, and the resulting acceleration trajectory is a non-geodesic of this manifold. If we now construct a manifold within which this curved

trajectory is a geodesic, we will find that, in this manifold, no forces are acting, and the object is simply travelling freely along the geodesic of the manifold, just like an object travelling inertially in Euclidian space. The interaction sets up the non-geodesic trajectory in the Euclician manifold by means of the well known condition in which the applied force is countered by an equal and opposite reaction generated by the acceleration, leaving a net force of zero. This zero force is the force acting along the trajectory, and hence within the manifold of which it is a geodesic.

Thus, the manifold picture represents the geometrical result of the force field picture, whereas the force field picture represents a view from another manifold (the Euclidian), from where the force field creates the manifold that constitutes the manifold picture. These two pictures thus represent the same reality viewed from two different manifolds. This argument can be applied to interactions of all kinds.

THE FORCE FIELD PICTURE AND THE MANIFOLD PICTURE:

The fundamental definition of a geodesic, via the fundamental geodesic equation, clearly belongs directly to the Calculus of Variations, which is a more general approach than that of the analysis of curved manifolds in that, although it implies the existence of a manifold of some kind, it can proceed without directly identifying the nature of the manifold, which may not be unique.

The Calculus of Variations, via Hamilton's Principle of Least Action, can also identify a trajectory in terms of a manifold (euclidian) in which it is a non-geodesic, although it will be a geodesic of some other manifold.

A smooth curved trajectory, as established by Hamilton's principle, or by the fundamental geodesic equation, may be a geodesic of more than one manifold. For example, a geodesic of the surface of a sphere is an equatorial trajectory or great circle. But this is also a geodesic of the euclidian surface of a

cylinder tangential to the sphere, having the same diameter as the sphere. The fundamental geodesic equation, that can identify the geodesic, need not specify whether or not it is to be thought of as a geodesic of the spherical manifold or the cylindrical manifold. This is because variations carried out within the surface of the sphere or within the surface of the cylinder will identify the same geodesic.

All this is an indication, and consequence, of the implication that the Calculus of Variations is more general and fundamental than the geometrical analysis of particular manifolds, and it might thus appear that the Calculus of Variations, in the form of Hamilton's principle, might even make the direct analysis of manifolds obsolete in practice. In fact, the matter does not allow such a simple conclusion.

I shall therefore proceed to a closer examination of the properties of the Calculus of Variations.

MANIFOLD ANALYSIS AND THE CALCULUS OF VARIATIONS:

I think that it is usual to begin with Hamilton's Principle of Least Action, and then show that it is really a form of the geodesic principle. Here, I shall work in reverse, and begin with the geodesic equation, and then develop the Principle of Least Action from it.

To do this, I will begin by gradually developing more complex forms of the fundamental geodesic equation, δds=0, in order to eventually connect it with the Principle of Least Action. This section, up to equation 4d, simply develops alternative, and more elaborate, but equivalent forms of the fundamental geodesic equation. These can prove useful, as will become clear in the section on the principle of least action. (Note that I use the form dsⁿ. Mathematical purists might object to this, but I use it on the basis that, if ds is infinitesimal, dsⁿ can be seen as infinitesimal also)

The fact that it can be shown that Hamilton's Principle of Least Action is merely a developed form of the fundamental geodesic equation confirms the fundamental role of the geodesic concept in nature.

Firstly, if δds=0 then

δds + δds + δds + ... = 0,                
or n x δds=0, or δnds=0               (1)

If ds is constant, we can have n = ds^n-1, so

δdsⁿ=0                                  (1a)

is a valid form of the equation and, similarly, as in (1),

δkdsⁿ=0                                  (1b)

and, if k = p^m,

δp^mdsⁿ=0                                  (1c)

Now, if the distance increments, ds, are not all equal to one another, it will make no difference to the geodesic equation, because the total distance will still identify a stationary value along the geodesic path compared to other paths. Therefore we can say

δΣds(s)=0,                             (2)

where the size of ds is some arbitrary function along a path s

Also, as in (1),

δΣnds(s)=0                             (2a)

and, as in (1c),

δΣp^mds(s)ⁿ=0                                  (2b)

(Here we use the summation Σ instead of , because ds has a functional and not an arbitrary infinitesimal

character, as implied by the concept of integration, although the maximum size of any value of ds(s) should be understood to be still very small).

Now we have, from (1), for the entire geodesic path.

Σnds(s) = nds,                     (2c)

where ds is now a constant. This can be made automatically true for any portion of the path, if ds is arbitrarily chosen such that it is always the case, for any ds(s), that *

ds(s) = ds                     (2ca)

(see top illustration in diagram). However, we can also put Σnds(s) in the equivalent form

Σnds(s) = n(s)ds,                     (3)

where n(s) is a value that changes along s, or is a function along s.

This will be achieved, for any portion of the path (see the centre illustration in the diagram), if we have

nds(s) = n(s)ds,                (3a)

for every ds(s). If this is the case, we may also have the equivalent

Σm(s)ds(s) = n(s)ds                     (3b)

if

m(s)ds(s) = n(s)ds                     (3c)

for every ds(s).

So we can have δn(s)ds = 0, with ds now a constant along s. I will put this in the general form

δf(s)ds = 0                     (4)

where f(s) is any function DEFINED ALONG THE PATH s

If we have f(s) = h(s)ⁿ, then δh(s)ⁿds = 0 and, since f and h are arbitrary, we can say, in general,

δf(s)ⁿds = 0                     (4a)

where n can have any value. If we have the case that f(s)^p= f(s)ⁿds^m-1, we can obtain

δf(s)ⁿds^m = 0                     (4b)

Since f(s) is arbitrary, at any value of s, we can put f(s) = k(s)^m, and (refer to centre illustration in diagram),

k(s)^mds = r(s)ds(s) = kds(s)^m,
where r(s) = kds(s)^m-1

and so

δΣkds(s)^m = 0                     (4c)

or, if we set r(s) = f(s)ⁿds^m-1,

δΣf(s)ⁿds(s)^m = 0                (4d)

This is the most general form of the developed geodesic equation, from which any of the others can be obtained by substitution. If, for example, we were to have ds(s) = ds, and m = 1, we would obtain the equation δf(s)ⁿds = 0, and similarly for other forms. (In such substitutions, of course, any forms that have ds(s) will have the Σ summation, and any forms that use ds will have the integral sign. However, I have kept the integral sign for forms involving dsⁿ).

*(Where Σ does not show limits, it is to be taken to refer either to the entire geodesic path, or any macroscopic portion of it).

THE FUNDAMENTAL GEODESIC EQUATION:

It is possible to write a fundamental geodesic equation of the form

δf(s)ds = 0

in the form

δf(s)ds = 0

This alternative form has a different conceptual meaning, which can be explained with the help of the illustration below.

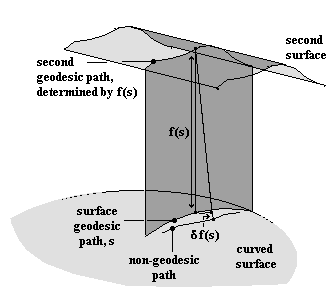
f(s) can be visualised as generating an area, standing vertically along the geodesic, with its height at each value of s determined by the value of f(s) at that point, and the area representing f(s). The height of f(s) thus creates a smooth curve of its own in space, and it is always possible to construct a surface of which this will be a geodesic. So, as shown in the illustration, we have two geodesics connected to one another by f(s). If, now, the surface path is varied away from the geodesic, as shown, the 'height'

of f(s), determined by connecting the upper geodesic to this path, will always be greater than the height determined by connecting it to the lower geodesic, by an amount that can be described as δf(s), as shown in the illustration. This quantity will thus be zero only along the surface geodesic, and this can therefore represent an alternative specification of the surface geodesic path.

The quantity δf(s) can be regarded as a total differential, made up of the partial differentials of its component variables, if it has any, in accordance with the usual total differential equation. This is the method that has been used to derive the Euler-Lagrange equations from the Lagrangian, L, which plays a similar role in a geodesic equation to that of f(s)

It is possible to use this method to combine a specification of multiple geodesic equations, along different geodesics, or a 'field' of such equations, such as

δf(s₁)ds₁ = 0
δf(s₂)ds₂ = 0

etc., into a single equation.

This can be done if the functions are simply added together to produce the following equation:

δ{f(s₁)+f(s₂)+f(s₃)+...}ds = 0

It is not necessary to include the ds values for each geodesic, provided the total lengths selected for all of the geodesics are equal to one another. In this case, a single increment ds can represent all the geodesics. Whether or not this equation, though mathematically valid, has any meaningful application to physical situations is another question.

AN ALTERNATIVE FORM OF THE GEODESIC EQUATION:

F(s)ds, at any location, s, represents a small segment of area under a curve along s, whose height is F(s). The longer the path joining A and B, the greater will be the total area F(s)ds. The value of the total area under the function F(s) will be minimised along the shortest path joining A and B - that is, along the geodesic connecting A and B. This will be represented by the stationary value δF(s)ds = 0, calculated within the manifold of which s is a geodesic.

The specification that F(s) is defined along s may mean that, at any particular proportion, or percentage, of the total distance, s, along any path connecting A and B, F(s) will have a value not less than that along the same proportion of the geodesic connecting A and B.

This is a sufficient, but not a necessary, condition. The necessary condition is simply that f(s)ds on alternative paths be not less than its value along the geodesic. The necessary condition is different because, if the value of the function f(s) along an alternative path is less than that along a corresponding part of the geodesic, the alternative path is longer, so that the value f(s)ds may still be minimised along the geodesic, in which case the equation δf(s)ds = 0 will remain true.

The argument in the first paragraph depends on this. It therefore does not prove that, in a field defined by F(x,y), the function F(x,y) will be minimised along a geodesic, s, joining A and B. This is because it cannot be said that, at a particular fraction of the total distance, s, along any path joining A and B, F(x,y) will always have a value not less than that at the corresponding distance along the geodesic connecting A and B, or, more accurately, that
F(x,y) will have a value not less than its value along the geodesic. This is because F(x,y) is not specified to be defined in terms of the distance s.

If, however, the function F(x,y) does always have a value along any alternative path, such that F(x,y) is never less than its value along the geodesic, then it will behave as the equivalent of a path-defined function.

If we define a smooth function, F(s), as being a function of a manifold within which it has a stationary value between A and B, we can say immediately that this indicates s to be a geodesic of some manifold, and F(s) to be a function defined along the path, s. If F(s) is defined along a non-geodesic of a manifold, it is then consequently to be called a function of some other manifold.

DEFINING A FUNCTION ALONG A PATH:

It will now be necessary to connect the foregoing geodesic equations with Hamilton's principle of least action, and we can do so by proceeding as follows:

Since we can put ds in the form (ds/dt)dt = vdt, we can say

δds = δvdt = 0

and, since we can multiply by a constant, we can say

δmvdt = δpdt = 0,

if m represents the mass of an object, and so we have a principle of least action applied to momentum. If we have (ds(s)/dt)dt, where the size of ds is a function along s, we will get

δp(s)dt = 0,

Since p(s) already contains v(s), we can multiply by v(s), without invalidating the equation, giving p(s)v(s), from which we get

δp(s)v(s)dt = 0,

and, since v(s) = ds(s)/dt, we get

δΣp(s)ds(s) = 0, which means δp(s)ds = 0

with momentum as a function along s. So, even if momentum is not constant, it will still follow a geodesic principle within the manifold within which s is a geodesic. We can manipulate p(s) in this way on the basis that it is a path defined function, since momentum always refers to the trajectory, or path, of an object.

Again, we can have

δΣds(s)² = 0,

so that

δv(s)²dt² = 0

and

δv(s)²dt = 0 since dt is a constant.

This, if multiplied by the constant, (1/2)m, with m signifying mass, becomes

δT(s)dt = 0,

where T is kinetic energy. This is equivalent to

δLdt = 0,

where L is the Lagrangian T - U, with U = 0, PROVIDED the variations are confined to the manifold in 3d space, in which the spatial trajectory is the geodesic.

So we have now reached at least one form of Hamilton's principle of least action. Note that, in the equation

δT(s)dt = 0,

with the kinetic energy changing along the spatial geodesic, s, the variations are confined to its manifold. If the variations exist, for example, within the manifold's euclidian embedding

space, this equation will not be true. But the equation

δLdt = 0

can be made to be true, within the embedding space, if we set L = T - U, with U having a suitable value not = 0.

We will then have

δLdt = δT(s)dt - dU(s)dt = 0,

where the variations exist in a euclidian space. This is a geodesic equation of a non-geodesic euclidian trajectory, and should, therefore, refer to a geodesic in some manifold. We shall see later that, in fact, the geodesic referred to here is that of the time coordinate itself.

If the variations are confined to the manifold of which the resulting trajectory of the test object concerned is a geodesic, we will have

δT(s)dt = 0

and, consequently also

δU(s)dt = 0

This allows the alternative form

δU(s)v(s)dt = 0

which can be put in the form

δU(s)v(s)dt = δΣU(s)v(s)(dt/ds(s))ds(s) = 0

so that

δΣU(s)ds(s) = 0

and

δU(s)ds = 0,

This shows that U(s) must be a field of such a kind as to be the equivalent of a path defined function, for variations confined to the spatial, geodesic-path manifold; otherwise the equation δU(s)ds = 0 would not necessarily be true.

What this means is that a potential energy field, U, must be of such a kind that it will support the equation, δU(s)ds = 0, within any manifold in which δds = 0 for the trajectory. Otherwise a particular, single, smooth trajectory could not be guaranteed for a test object in a potential energy field.

By a similar argument to that for U(s), we may obtain

δT(s)ds = 0

along the spatial trajectory, though only for variations confined to a manifold of which s is the geodesic.

It is thus a potential energy field, in conjunction with the velocity of a test object, that specifies a local manifold, of which the trajectory is a geodesic, and this applies to all fields.

HAMILTON'S PRINCIPLE OF LEAST ACTION:

Since a trajectory is fully determined by Hamilton's Principle of Least Action in euclidian space, the question arises as to whether the manifold concept is really relevant at all. That is, is it merely an academic mathematical construct, divorced from being any actual property of the reality itself?

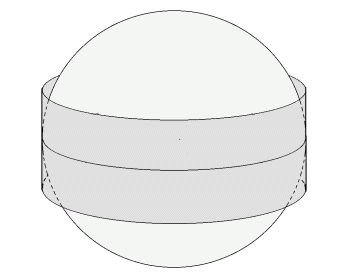
This is reinforced by the consideration that a geodesic trajectory can be a geodesic of both a curved surface and its curved euclidian tangent surface, at the same time, as represented by the sphere and enclosing cylinder, respectively, in the figure above, and, wherever variations are specified as restricted to the surface of which the trajectory is a geodesic, either surface can be used. This appears to indicate that the variational principle might have, as it were, a primacy over the

manifold concept, possibly making the manifold concept irrelevant.

To answer this, it may be remembered that the trajectory of a test object is set up by a force field interaction with the object, that is balanced by the object's inertial response. This establishes not only an acceleration trajectory in euclidian space, but also the accumulation of kinetic energy and momentum. Since these, once acquired, are properties of an object, insofar as it retains the quality of a free object, and not features of the interaction itself, they must be established geometrically, and therefore on the basis of a geodesic of some kind, whether euclidian or not.

It follows therefore that, if the trajectory is not a euclidian geodesic, owing to the interaction taking place, it must be the geodesic of some other manifold, in order that the geodesic equation
δT(s)ds = 0 is enabled to be true, independently of the interaction.

That is to say, we have seen that δT(s)ds = 0 and δU(s)ds = 0 must be independently true for variations occuring within a manifold of which the resultant trajectory is a geodesic. This, in fact, shows that nature has to identify and create some kind of manifold geodesic, that is able to be seen as distinct from the interaction, in order to establish the kinetic energy as something preserved independently of the interaction itself.

WHETHER OR NOT THE MANIFOLD CONCEPT IS RELEVANT AT ALL:

While a test object is travelling on the geodesic of a 3-d manifold in physical space, it must also, for a similar reason, be travelling on a geodesic of a 4-d manifold in 4-d space, if time is a dimension of a 4-d space.

Since the equation δds² = 0 is true for a trajectory, ds can be identified as an element of distance in 4-d space just as well as for a 3-d space. Therefore we can have the equation in the form (using Galilean spacetime here)

δ(dx² + dy² + dz² + dt²) = 0

This can be written

δ(ds² + dt²) = 0

Since we know that δds² = 0 independently, we must have

δdt² = 0

and therefore

δdt = 0

That is to say, any trajectory involves a distinct geodesic as a component in the direction of time, with the time itself, t, being subject to the fundamental geodesic equation. Since the above equation can be multiplied by a function, and we know, according to Hamilton's principle, that

δLdt = 0

we have the conclusion that Hamilton's Principle of Least Action is, in fact, the direct expression of a geodesic equation, in which the geodesic distance is being measured along the time coordinate, instead of being measured in a spatial direction, in the usual way, with the time coordinate itself being seen, here, as a geodesic in the direction of time. It follows also, of course, that the Lagrangian, L, has to be seen as a path-defined function in the direction of time.

THE 4-D TRAJECTORY:

© Alen, March 2007; update Dec 2010.
June 2019 - re-engineered to display properly on Chrome and Firefox
alen.1@bigpond.com

Material on this page may be reproduced
for personal use only.