The Spacetime Diagram in Special Relativity

THE SPACETIME DIAGRAM AS AN ILLUSTRATION OF THE FAILURE OF MINKOWSKI SPACETIME

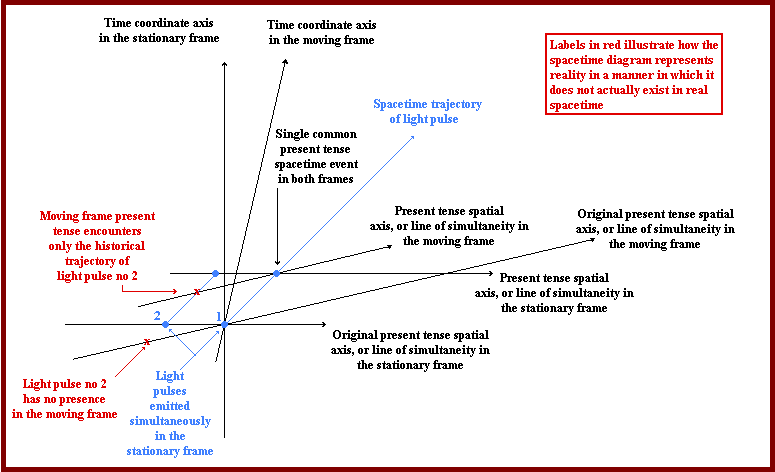
FIGURE A

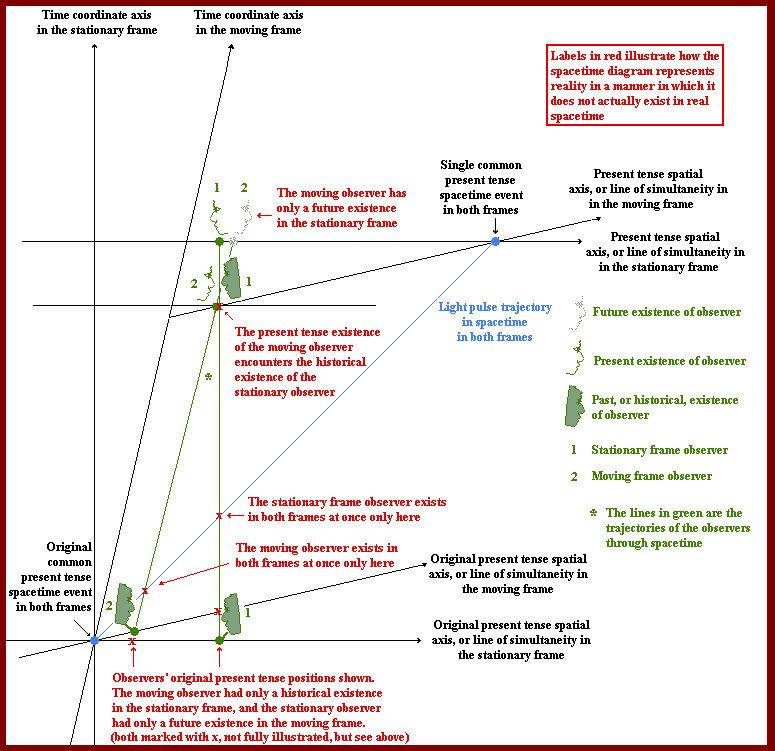
FIGURE B

NOTES ON THE NATURES OF PAST AND FUTURE:

There are two possibilities regarding the past and future:

1) They have a real existence along a real spatial-like time coordinate,

2) They do not really exist at all.

In the latter case the past and future are just ideas and have no real existence. In the diagram, therefore, the past and future observers simply would not exist at all, and the spacetime diagram fails for that reason.

If the first alternative is true, then a spatial-like time coordinate is an actual reality, and it is necessary to consider the nature of the past and future existences of an observer.

It should be easy to understand that anything in the past must be something entirely unchangeable. One cannot modify anything that actually happened. If, for example, money was stolen, nothing can ever change the fact that the theft happened. In the past, therefore, the realities become fixed and unchangeable and, in short, are realities no longer subject to the laws of physics.

A similar consideration can be applied to realities in the future. They can be changed only via the present, and not directly. If a driverless truck, for example, is careering down a hill, the destruction of the house

at the bottom of the hill can be avoided only in the present tense, as, for example, if someone manages to jump aboard the truck and put the brakes on. So future objects are also not directly subject to the laws of physics. The laws of physics apply only to objects in the present and, indeed, this can be used to define the meaning of the word 'present' and, consequently, 'past' and 'future' also.

Any portrayal of a spacetime, therefore, as in the case of the spacetime diagram, and the Minkowski spacetime it represents, that involves a present observer encountering any observer or object in the latter's past or future cannot be a true portrayal of the spacetime that actually exists. Objects in spacetime interact according to the laws of physics only with other objects also subject to the same laws of physics. That is, only present tense objects can interact with one another and any model of spacetime must reflect this basic truth.

P.S. I favour the view that the past really exists, not in the same manner as the present, but like a kind of perfect, full-size 3D movie record. In this case, if it were possible to return to the past (not via material reality, subject to the ordinary laws of physics, but perhaps for disembodied, spiritual beings) and move forward alongside it, without interacting with it, since it is unalterable, it would be possible to view the entire, full-size, 3D history of the cosmos from its beginnings.

A CONCEPT OF SPECIAL RELATIVITY IN GALILEAN SPACETIME:

The above diagram is taken from this page on Einstein's original derivation of the Lorentz transformation equations in Special Relativity. The relevant diagrams that illustrate the Light postulate are Fig 1, showing a light pulse trajectory in a moving frame and Fig 2, showing the same light pulse trajectory in the stationary frame. Such trajectories of the same pulse are impossible in ordinary galilean spacetime, so Minkowski spacetime was invented to solve this problem.

Since, however, as illustrated by the diagrams in the previous section, Minkowski spacetime cannot work in reality, as a real spacetime, it is necessary to try to return to galilean spacetime to see if a way can be found to implement the light postulate, in spite of the apparent impossibility.

The only way in which, it would appear, that this can be done is if we suppose that a single light pulse is not really the single, simple entity it has been assumed to be. That is, if we suppose light to be a multi-component reality, with separate components of the same light pulse existing in separate, relatively moving frames, then we can suppose that the light pulse trajectory in Fig 1

identifies a distinct and separate component of the same pulse to that identified by the trajectory shown in Fig 2. This will enable the light postulate to be implemented in galilean spacetime without any difficulty.

Obviously, if these trajectories describe separate components of the same light pulse, they must be linked together by a previously unknown internal structure within light itself. In addition, it can be said that the spacetime events identified, at any moment, by the component pulses in the two frames are related by the Lorentz transformation equations, which therefore give a mathematical description of this unknown internal structure within light itself.

It might also be remarked that, in this implementation of the transformation equations in galilean spacetime, they no longer represent simple coordinate transformations of a single event, as with Minkowski spacetime, but are mappings of a spacetime event in one frame to a different spacetime event in the other.

All this was originally dealt with more fully on the page on Special Relativity as a Theory of Light

Material on this page may be reproduced
for personal use only.