
AN ENQUIRY INTO THE POSSIBLE MEANING
OF THE SR (LORENTZ) TRANSFORM
IN THE ACTUAL, DYNAMIC REALITY.
This page is intended to demonstrate that it cannot be simply assumed that the meaning given to the SR (Lorentz) transform in the actual, dynamic reality will be automatically the same as that which has been given to it in the abstract, static, purely geometric 4-d spacetime.
Since it has been shown that the SR transform can be derived as a 4-d coordinate transformation in a static background spacetime, without using the light postulate, and dynamic-based derivation, originally used by Einstein, it has been supposed that this is the most fundamental, underlying reality behind the properties of the transform in the dynamic reality.
However, it needs to be understood that the static
spacetime model has conditions markedly different from the dynamic reality in that it does not have any of the restrictions on time coordinate values that are inescapable in the actual, dynamic reality.
It should not, therefore, be merely assumed that the coordinate transformation in the static, background spacetime automatically applies to the dynamic reality, without the need for any further consideration. It is particularly important to closely examine this matter in that the purpose of the theory of special relativity is to gain an understanding of the dynamic properties of physical objects in relative motion rather than to understand merely a purely abstract, background model.
SUMMARY:
This examination of the SR transform will pay particular attention to the transformation of the time coordinate, on account of the fact that there is no particular problem with purely spatial coordinates. This will involve an examination of the transformation of the time coordinate between two relatively moving inertial frames, in which two observers in the two different frames are located at the same locations as their individual clocks, and both clocks were set to zero when they were spatially adjacent to one another.
The purpose of using this particular form of the time transformation is that it involves, mathematically, only the times, with no spatial distance component in the equation. What can be clearly concluded from this particular case will automatically have a similar implication for other forms of the time transformation, without the need to examine them directly. The time transformation equation, under these conditions, has the form:
τ = (1/γ)t
with τ the time coordinate in the moving frame, and t the time coordinate in the 'stationary' frame.
Having got these preliminary remarks out of the way, I put the question to be examined: can the SR transform mean the same thing in the dynamic reality that it can in the abstract, static, geometrical spacetime? In the abstract spacetime no limitations are imposed on time coordinates, but in the dynamic reality there is always a severely restricted access to any time coordinate axis, because of the fact that any observer can access only his own present tense time coordinate at any particular moment. Therefore, it is necessary to ask : does this impose any limitation on what the SR (Lorentz) transform can mean in the actual, dynamic reality, as compared with the abstract, geometrical spacetime?
To answer this it is necessary to start with the standard SR theoretical supposition that, in the abstract, geometrical spacetime, the SR transform is a simple 4-d coordinate transformation of a spacetime event from one spacetime reference frame to another.
In the dynamic reality, however, a spacetime event, as an abstract geometrical point in spacetime, is selected or identified by some physical event of a transient, momentary kind. To take a concrete example, let us suppose we have our two relatively moving observers located at the positions of their clocks, in the manner mentioned before. Now let us suppose a spacetime event is identified by a pulse of light striking, and reflecting off, the moving observer's clock. This will identify the geometrical event as having the moving time coordinate indicated
by the time on the moving clock, in the present tense of that clock and its observer.
Now, it must be supposed, in accordance with the standard SR spacetime theory, that the time shown on the stationary observer's clock will also be a present tense time for the stationary observer, with the two times, although different, being related by the SR time transformation equation.
This present tense requirement is based on the standard supposition that a light pulse is a single entity, independent of the reference frame to which its location at any moment is referred. It is equally present to all observers in all reference frames, and identifies the geometrical spacetime location once only. That implies that any time coordinate that describes its location at any moment is always a present tense time coordinate belonging to the relevant reference frame. In other words, since the physical event happens once only, and not twice, and happens for every observer, it cannot be in the present tense for one observer, and in the future tense for another. If it were, then it would later occur in the present tense for the other observer, and the light pulse must be at the same spacetime location a second time.
For the same reason, it cannot be in the present tense for one observer and in the past tense for another, which is just a different way of saying the same thing.
This imposes a severe limitation on what a time coordinate can be on either side of an SR time transformation equation, and I have shown that it cannot be met in the actual, dynamic reality. On the Minkowski time intervals page I have shown, mathematically, that, in the circumstance described above, where both observers are located at the positions of their own clocks, both times, on both sides of the SR time transformation equation can NEVER both be present tense times for both observers. This immediately implies that, although the SR transform can be a simple 4-d coordinate transformation in the abstract, static, geometrical spacetime, it cannot be such a coordinate transformation in the actual, dynamic reality, and be in accordance with the suppositions of the standard spacetime theory.
This leads to the question: what, then, can the SR time coordinate transformation mean in the actual, dynamic reality?
To begin with, let us examine how, in general, any ordinary geometrical coordinate transformation can be made to mean something else, without making any change to the actual mathematical form of the transform.
THE SR (LORENTZ) TRANSFORM:
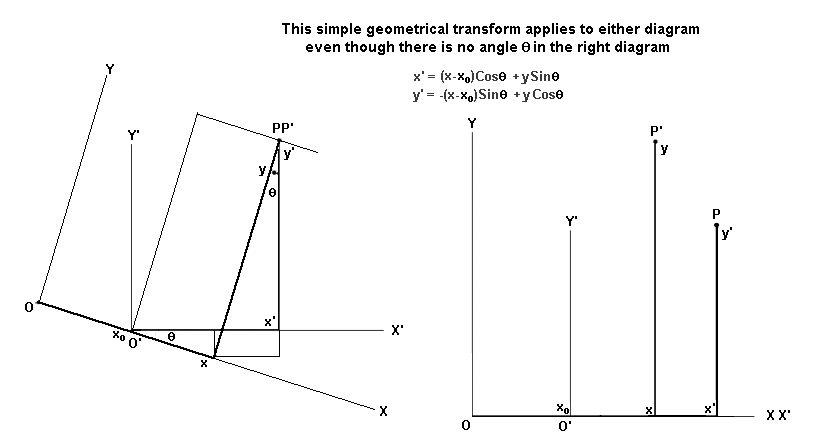
In the above simple 2-dimensional geometrical coordinate transformation, shown on the left, the mathematical transform shown transforms the coordinates of the reference frame with origin O(x,y) to the coordinates of the reference frame with origin O'(x',y'), in which x' and y' are given as functions of x and y. The geometrical point for which the coordinates are given in either frame is the point P or P', which are different labels for the same point. A different geometrical meaning can be given to this transform by simply separating P and P' into two distinct points, as shown on the diagram to the right. This causes the transform to become a mapping of the coordinates of the point P to those of the now different point P'.
Note that there is no mathematical change of any kind to the transform itself. The diagram on the right also indicates only one possible way of separating the points P and P', but it is enough to illustrate the basic concept.
The above simple, geometrical illustration is not intended to relate directly to the SR transform, except in so far as it illustrates that the meaning of the SR coordinate transformation can be given another meaning simply by separating the spacetime point, or 'event', into two distinct spacetime events, in the same way in which P and P' are made to become two distinct geometrical points.
If the SR transform is converted in this way, so that it is no longer a coordinate transformation of one spacetime event, then the fact that the time coordinates on both sides of the time transformation equation cannot both be present tense coordinates no longer prohibits applying the transform to the actual, dynamic reality.
It can be said, therefore, that in the actual, dynamic reality, the SR transform MUST be a mapping between the coordinates of two different spacetime events.
It is no doubt possible to create a transform that will be a coordinate transformation of a single geometrical spacetime point in which, in the dynamic reality, the time coordinates will be present tense time coordinates in both frames, but such a transform will not be an SR, or Lorentz, transform, but a transform of some other kind.
It is necessary, of course, to find a way to identify the two distinct spacetime events that are related by the SR transform.
We can begin by recognising that the original transform was derived by Einstein in a dynamic reality, in which light, and its peculiar light postulate, played the crucial role. All the dynamic observations that led to the equations did so via the communication of information, via light, to one observer, or reference frame, or to the other. The key, therefore, to understanding the transform in the dynamic reality is to recognise that it has to do with the communication of coordinate information, and that it may be a matter of a communication from one frame to the other, i.e., from the moving frame to the stationary frame, or vice versa.
Let us, by way of illustration, take, as an example of communication, a communication within a single reference frame. If I have a panel of lasers, arranged to be able to be switched so as to display the time, in figures, at my location, and I fire a set of pulses, showing this time, to a light receptor panel 1km away where, let us say, you are, then your panel will receive, and record, my time a little later than it actually occurred. Both the initial laser pattern, when sent, and the later reception of it, when received, identify two distinct spacetime events. As events, they are entirely equal to one another, but in terms of the existence of dynamic communication, I may call the initial event, an event simply, and the later, reception event, an observation event, because it can observe information established at the initial event.
I can, of course, also observe the initial event myself, and so it can also be an observation event as well. In my case the time coordinate of the initial event as an event simply, or as an observation event, is identical.
The reception event, as an observation event, has a different time coordinate, since it occurs a little later than the initial event. I can, therefore, characterise communication as being a relationship between events defined as observation events or, simply, observations, of some initial event as dynamically defined.
We have to consider, therefore, that the separation of the supposed single spacetime event into two distinct events, in the dynamic operation of the SR transform, may be a separation of observations of some initial event whose identification is caused by some material reality stationary in some particular reference frame.
In the example suggested, in which the initial event is defined by a light pulse striking the moving observer's clock, the clock is stationary in the moving frame, and not in the stationary frame. The coordinates which the SR transform defines for the stationary observer's frame can therefore be regarded as a stationary frame observation event of the original moving frame (dynamic, physical, momentary) event, which occurred in the present tense of the moving frame, at the location of (and defined by) the moving clock.
Since the original event is, by definition, in the present tense in the moving frame, its observation event time coordinate in the stationary frame will not be defined as a present tense event in that frame, but can be called only a derived event of the original event, even if it does, later, become present in the stationary frame. In other words, since we have shown that the time coordinate in the stationary frame cannot be a coordinate of the original event, it must be a coordinate of a stationary frame OBSERVATION of the original event, which is distinct from the original event.
If, for example, the observation event in the stationary frame is initially defined by the SR transform as a future tense time coordinate in that frame, then it will later become a present tense coordinate in that frame, when it will be actually observable by the stationary observer. At that time, the time coordinate of the original event, as described by the SR transform, will then have become a past tense time coordinate in that frame, for the moving observer.
So we see that Special Relativity, in the dynamic interpretation, creates a separation between an original event dynamically defined in the present tense in one frame, and its observation event, not defined in the present tense, in a relatively moving frame, which is not caused by the spatial separation of the events, and is not a function of such a separation, but is an entirely different separation of an event from its observation event, caused by the relative motion of the two frames, and is a function (expressed by the SR transform) of that relative motion only.
To be clear about all this, the distinction must be kept in mind between what the concept of an event is defined to mean in the abstract, background spacetime, and what it is defined to mean in the actual, dynamic reality, involving real objects as the means of identifying dynamic events. The two different meanings are connected, of course, in that the momentary, dynamic event also identifies, or selects, an event belonging to the abstract, background spacetime
So we have shown that the SR transform, when applied to the actual, dynamic reality has to be given a meaning different to that which it can be given, and normally is given, in the abstract, static, 4-d geometrical spacetime.
Since, as has been shown, the SR transform, in the dynamic reality, is not a coordinate transformation of a single spacetime event, it is of interest to ask: what form would such a single-event coordinate transform take in the dynamic reality?
Firstly, the general form of the SR transform is given by:
ξ = γ(x-vt)
τ = γ(t-vx/c2)
η = y
ζ = z
Now, (x-vt), in the first equation above, is the stationary frame length contracted version of the moving frame proper length, ξ. The stationary frame value, x, identifies the stationary frame spatial coordinate of the stationary frame observation event corresponding to the original, moving frame event identified by the moving frame spatial coordinate ξ. These events are dynamically defined, but also identify events in the background spacetime.
The event for which we want to find the coordinate transformation is that defined by the SR transform coordinates (ξ, η, ζ, τ) in the moving frame. In the stationary frame, this event will not have the SR transform coordinates (x, y, z, t)
To find the stationary frame coordinates, we may note that the length contracted distance x-vt is associated with the stationary frame observation event. The original event, in the stationary frame, would therefore be identified by a non-length-contracted value γ(x-vt). So therefore the spatial coordinate in the stationary frame would not be x, but
x'=vt'+γ(x-vt)
thus giving the spatial coordinate transformation for ξ as
ξ=x'-vt'
where t' is the stationary frame present tense time, since a coordinate transformation requires the coordinate times in both frames to be present tense times, as argued already.
The spatial coordinates y and z would be the same in the SR transform and in the true coordinate
transform, as these are not affected by the relative motion in either case.
It has been shown in the Minkowski time intervals page, mentioned before, that the actual present tense times for all relatively moving observers remain the same, and this time must therefore be used, in both frames, for the true coordinate transform. Therefore the stationary frame time corresponding to the moving frame present tense time, τ, would be t' rather than t, where t' = τ. So therefore the true coordinate transform, in the dynamic reality, writing x' as x, and t' as t, will be given by:
ξ= (x-vt)
τ = t
η = y
ζ = z
In other words, the true coordinate transform in the dynamic reality is simply the Galilean transform. Here, the stationary frame coordinates (x, y, z, t) are, of course, not the same as those used for the SR transform.
It must be noted, however, that this does not negate the action of the SR transform, since communication between relatively moving frames cannot occur via the Galilean transform, but by the SR transform only. That is, all observations, and also all interactions between relatively moving inertial frames via lightspeed bosons, can occur only via the SR transform, and not via the Galilean transform, even though the Galilean transform is the true coordinate transformation in both the dynamic reality and in the background spacetime. The SR transform connects the coordinates of an original event with the coordinates of its separate observation event, in a relatively moving frame. The original moving frame event is not directly observable from any relatively moving inertial frame.
If, in the case of interactions, which cause acceleration, and make a relatively accelerating frame to be non-inertial, we can model acceleration, from an inertial perspective, as a stepwise transition from one relative velocity to a slightly different relative velocity, then we can suppose that interactions will be determined in accordance with the SR transform, and perhaps also in accordance with Lorentz invariant values associated with the accelerating frame.
WHAT COORDINATE TRANSFORM WOULD BE VALID IN THE DYNAMIC REALITY?:
The so-called 'spacetime interval' is a concept closely associated with the abstract, purely geometrical, background spacetime model. It is supposed to be a fundamental invariant in SR. The equation that describes the spacetime interval is given as:
(cdτ)2 = (cdt)2 - dx2 - dy2 - dz2
which can be written, in a shorter way, as
(cdτ)2 = (cdt)2 - ds2
Now, this can arbitrarily also be written as
(cdτ)2 = -(cdt)2 + ds2
on the understanding that (cdτ)2, which identifies the spacetime interval, can be either positive, negative, or zero.
All the various arguments and descriptions of the spacetime interval, which you can find easily by searching on the internet, is a result of a total divorcing of the abstract spacetime model from the dynamic reality. It does nothing to illuminate the mind about this reality, but actually only serves to create meaningless confusion.
The fact that the SR transform can be derived non-dynamically in the static, 4-d, background spacetime does not imply that this abstract concept HAS to be the more fundamental reality, of which the observed reality is just a manifestation, as it were. Such an assumption is a serious mistake, and the previous arguments show that the abstract model is not consistent with the dynamic reality, which cannot, therefore, merely be its dynamical manifestation.
So let us ask what, in the dynamic reality, corresponds to the so-called spacetime interval?
In the following form of the equation (which is the
only meaningful form in the dynamic reality):
(cdτ)2 = (cdt)2 - ds2
dτ and dt are times in a moving and stationary frame respectively. As mentioned before, only one of these times can be a present tense time, and we can write two equations with the present tense time being arbitrarily specified to be dτ in one equation and dt in the other.
Now, if we specify the equation in which dτ is the present tense time, then dτ, and cdτ are invariant from the perspective of any inertial reference frame.
In the dynamic reality, therefore, the significance of what corresponds to the 'spacetime interval' is that dτ is the present tense time in the reference frame of the clock which measures it.
dτ is positive in the dynamic reality, which means that relative motion is less than the velocity of light, and events are related in a timelike manner. If dτ could be zero, dynamically, then it would specify the existence of a relative motion equal to the velocity of light. If (cdτ)2 could become negative, then it would specify the existence of a relative velocity greater than the velocity of light, which is not allowed in SR. In other words, in such a case, the above equation becomes simply meaningless, invalid, and inapplicable, in the dynamic reality.
All this means that the spacetime interval concept based on the abstract, background, 4-d spacetime is a purely theoretical concept entirely divorced from the actual dynamic reality. Rather than illuminating this reality, which is what is of interest, it creates only a complicating and confusing irrelevancy, creating an arena for the discussion of all kinds of pointless details and considerations, which can have only a purely theoretical interest.
THE SO-CALLED 'SPACETIME INTERVAL' IN THE DYNAMIC REALITY:
© Alen, September 2014.
june 2019 - re-engineered to display properly on Chrome and Firefox.
alen.1@bigpond.com
Material on this page may be reproduced
for personal use only.