Mathematical Proof that Minkowski Equation Time Intervals Cannot Represent Current Time Intervals for Both Observers in Both Frames.

The illustration below indicates an experiment in which observers A and B, with their rocket ships, are initially at rest in observer C's reference frame, located with observer C at origin O, and all three observer's clocks are synchronised to zero. At this moment, A and B almost instantaneously accelerate, simultaneously, to velocity v relative to C, in directions at right angles to one another, with A accelerating in the negative x direction and B accelerating in the negative y direction. This means that, in A's reference frame, C is travelling in the positive x direction, and, in B's reference frame, C is travelling in the positive y direction.

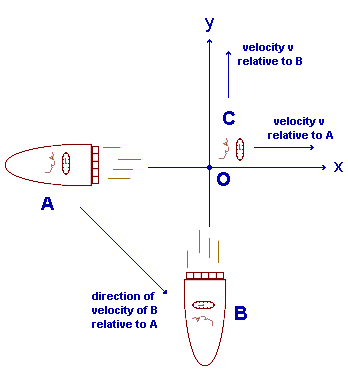
We must now examine the relationships of the time intervals associated with the different observers. The times on the clocks express the time intervals each observer has experienced, whether currently or otherwise, since the accelerations ceased, which is virtually the same as that since the accelerations started, since the accelerations were as close to instantaneous as possible. That is, at the termination of the accelerations, all the observers' clocks can be taken to be all reading zero, on the basis that any times shown will be negligible compared to the readings on the clocks in the situation shown in the illustration.

The general Minkowski spacetime equation that relates a moving frame time interval to that in a stationary frame is

c²dτ² = c²dt² - dx² - dy² - dz²

where dτ is a 'proper' time interval on a moving clock. That is, it is the time interval between two moving clock times, as shown on the moving clock in its own reference frame. dt is the time interval shown on a stationary frame clock, that measures the stationary frame time interval between the two times, or events, measured by the moving frame clock. That is, the time interval dt, in the stationary frame, is a stationaryframe measurement of the time interval dτ, in the moving frame. We shall arbitrarily specify dt to be a 'current' time interval in the stationary frame. dt will therefore be the current time on a stationary clock, if the clock was initially set to zero at the start of the measured time interval. We shall, in this way, specify that the clock A is to be taken as showing the current time to observer A in his own frame, and this will lead to the conclusion that clock B is also showing the current time to observer B in his own frame.

dx, dy, and dz, are stationary frame spatial intervals corresponding to the time intervals. These

measure spatial distances travelled, if they started at zero at the start of the measured time interval

For observer A, in the illustration, observer C is moving along the x axis only, so the general equation becomes (setting c = 1)

dτ_c² = dt_a² - dx_a²

For observer B, in the illustration, observer C is moving along the y axis only, so the general equation becomes

dτ_c² = dt_b² - dy_b²

and we have |dt_a| = |dt_b|, and |dx_a| = |dy_b|

Since A and B have identical relationships with C, as far as the quantities in the equations are concerned, and we have specified that dt_a shall refer to the current, or 'present', time for A, in his reference frame, we must conclude that dt_b also specifies the current time for B in his own frame. dt_a and dt_b are therefore the current times for both A and B, which they see on their clocks, since the stationary frame clocks have been set to zero at the start of the measured time intervals. The current time for both A and B is therefore the same, since |dt_a| = |dt_b|.

However, since A and B are moving, relative to C, in orthogonal directions, they also have a velocity relative to one another, so that, if A is taken as a stationary frame, B is moving relative to him, and we will have the following equation relating time intervals in the two frames, A and B:

dt_b'² = dt_a² - dx_a² - dy_b²

This means that dt_b' cannot be equal to dt_b, since dt_b is already known to be equal to dt_a. dt_b' cannot, therefore, be a current time interval in frame B, because we already know that dt_b is the current time interval in frame B. Yet, in accordance with the definition of the equation, dt_b' must refer to a proper time interval in frame B. This proper time interval cannot, therefore, be the current proper time interval for observer B. The implication of this is that dt_c also cannot be a current time interval for observer C. In other words, it follows that this argument has proven that the moving frame proper time interval, as specified by the Minkowski equation, can never refer to a current moving frame time interval, if the corresponding stationary frame clock is referring to a current stationary frame time interval.

This has implications for the solution normally offered in answer to the twins paradox, because it means that the accumulated moving frame time interval cannot represent the current moving frame time interval for the travelling twin, when he arrives back home. It cannot, therefore, be used to specify his current age on his arrival home.

There is a further argument about the real meaning of moving and stationary frame time intervals in the link to my Twins Paradox page below.

A Note on 'Current' Time Intervals: The 'current time interval' concept is used to mean a time interval, in an observer's own frame, that terminates in the observer's current, or present, time. It is distinguished from what would be a 'future time interval', which would be a time interval that is completed, or terminated, in the observer's future, whether or not part of the time interval includes the observer's present. Likewise, a 'past time interval' would be a time interval that was terminated in the observer's past.

Mathematical Proof of a Universal
Current Proper Time for All Inertial Observers

The foregoing section showed that the SR transformation equation time intervals, in the Minkowski version of the time transformation, do not represent current time intervals in both of any two inertial frames in relative motion. The transformation equations cannot, therefore, be used to give the current time interval in observer C's frame, by means of the current time intervals in the frames of observers A or B. Let us ask the question, therefore: can we determine what is this current time interval in observer C's frame?

In the illustration below, a fourth observer, C', has been added, such that the velocities of B and C, relative to C', both have the value v/2. Here, C' also commenced accelerating, in C's frame, simultaneously with the other observers, at origin O.

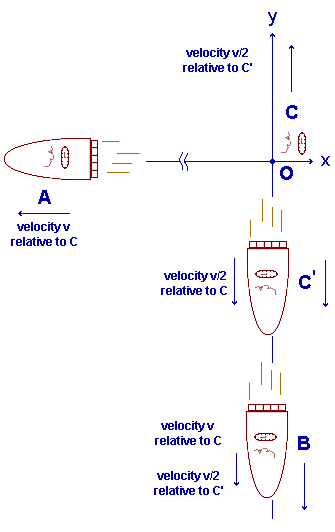
The result of this is that observer C' is half way between observers C and B. Since observers C and B thus have identical relationships to observer C', in the same way that observers A and B have identical relationships to observer C, we can say that the time intervals for observers B and C must be the same as one another, in the same way that those of A and B are the same as one another. If, now, the time interval is a current time interval in observer B's frame, which has been shown already, then the time interval for observer C, in his frame, which is the same as that for B in his frame, must be the current time interval for observer C. Thus, we have proven that the current time interval in observer C's frame is the same as those for observers A and B. All three have the same current time interval as one another.

An identical argument can be used to show that the current time interval in the frame of observer C' must be the same as those for observers B and C. Thus we have shown that the current time intervals in the frames of all the observers A, B, C, and C' are identical to one another. Since the velocity v is arbitrary, we must conclude that the current proper time intervals for all inertial observers, in all inertial frames, are all equal to one another.

The limitation on this conclusion is that all these inertial frames accelerated simultaneously, from a

common origin O. The question is: would this conclusion apply to inertial frames that accelerated, from origin O, at an arbitrarily different time to the time at which the other observers did so?

To answer this, it may be observed that we have established that an observer, such as A, in A's frame, will have the same current time interval on his clock as does observer C, in C's frame. This now allows examining the relationship between A and C, without any further need to involve a third observer, like B. Thus, we can say that any observer, A, who accelerates from origin O, at any time, if he has a clock identical to that of observer C, at O, will always have a current time, within his own frame, identical to that of observer C, who remains in the original 'stationary' frame at O. This means that the limitation, mentioned in the previous paragraph, no longer applies to the conclusion that the current proper time intervals for all inertial observers, in all inertial frames, are all equal to one another.

We may, however, go one step further, and ask the question: what if A accelerates from observer C's frame at some arbitrary location, O', other than O, where C is located?

To answer this we suppose that observer C has an array of clocks, stationary in his frame, all synchronised with one another, including one at location O'. It follows from what has been said already that, if A has a clock identical to any of those in the array in C's frame, and accelerates from O', into an arbitrary inertial frame, his clock will always retain the same current time as the clock at O', in C's frame.

Since the clock at O' defines the proper time in C's frame, and A's clock defines his proper time in his frame, we have established that the current proper time for all observers in all inertial frames is always one and the same.

This result does not invalidate the SR transformation equations because, as has been shown in the first section above, the time transformation equation, in the contexts shown, never relates the current proper times in both of two inertial frames at once. If the equation represenst the current time in one frame, it will always relate this to a past or future time in the other.

This scenario, used in the foregoing arguments, applies to clocks that were originally located together, in one frame, before one of them accelerated into a moving frame, and which are related to one another by the transfromation equation for time, in the form of the Minkowski equation. If, however, a stationary observer uses light to examine different clocks in an array of moving clocks, all synchronised with one another in the moving frame, he will observe an apparent nonsimultaneity effect in the moving frame. This, however, will not affect the conclusion of a universal current proper time, based on the particular clocks used, which were the most suitable for the argument.

It may be remarked that the existence of a universal proper time across all inertial frames is consistent with a galilean-type spacetime, but not with a Minkowskian-type spacetime, which suggests that the results (both mathematical and experimental) associated with the SR transformation equations must be expressing something other than the properties of an underlying Minkowskian-type spacetime.

© Alen, March 2007; update Dec 2010.
June 2019 - re-engineered to display properly on Chrome and Firefox
alen.1@bigpond.com

Material on this page may be reproduced
for personal use only.