A NEW FUNDAMENTAL GEODESIC PRINCIPLE
IN GEOMETRY AND PHYSICS

The great problem in the traditional analysis of curved manifolds was the fact that the only originally available geometry was Euclidian geometry.

This meant that the mathematics of any other geometry, such as that of curved surfaces, had to be constructed out of Euclidean mathematics, and the result was that a Euclidian geometry of a flat embedding space had to be used in order to describe the geometry of a curved surface within it. This allowed the construction of the well known First and Second Fundamental Forms, to describe the properties of the curved surface.

Attempts were made by Gauss and Riemann in the direction of constructing a geometry wholly intrinsic to a curved surface, that is, without reference to any embedding space. I haven't been able to find a work that makes clear the degree to which this was actually successful.

Riemann, for example, used the property that a

vector parallel transported around a closed loop, upon a curved surface, from a point, P, back to the same point, P, changes direction in a manner determined by the curvature of the surface. This process itself is wholly intrinsic to the surface. Nevertheless, Riemann's curvature tensor derived from this process uses the Christoffel symbols, and I do not think that it has been made clear whether or not these can be derived entirely from within the surface itself. They are usually derived either from the two fundamental forms, which involve the surface embedding space, or by some other means, also using the embedding space.

The question, therefore, that I ask, is, could a geometry of a curved surface be discovered from a perspective entirely confined within the surface itself? In what follows I will consider how this question might be given a clear, unambiguous answer.

PART 1 - THE GEOMETRIC ARGUMENT:

I shall first set up a scenario that will establish what we are to mean by a perspective confined to being wholly within, and thus intrinsic to, a curved surface. To do this I introduce the concept of so-called 'flatlanders', that is, two dimensional beings confined to the two dimensional arena of a curved two dimensional surface. The light they see is only that which travels within the surface, and they can see only two dimensional objects that exist within the two dimensional surface. This is what will be meant by the flatlanders 'perspective', also called an 'intrinsic perspective', to mean that it is confined to their two dimensional surface.

This scenario is somewhat problematic to visualise, as two dimensional beings can see only the one dimensional edges of two dimensional objects within the surface. We, in a three dimensional world, likewise see only in two dimensions, one dimension less than the world itself. Stereo vision is a contrivance that allows us to create a three dimensional interpretation of what we can see two-dimensionally.

In order to facilitate visualisation of the discussion, I will introduce a modification of the flatlanders experience by allowing them a very small thickness in a third dimension. This is to be considered such as will allow at least some of the very thin two dimensional objects to slide over one another in the very thin third dimension, and allow the flatlanders to see the two dimensional objects from slightly above them, just sufficiently to gain an impression of their two dimensional shapes. This will not, however, allow arbitrary movements of any kind in the third dimension, or release any objects from their conformity to the curvature of the surface. That is, this contrivance does not allow the possibility of three dimensional measurements of any kind; but it will help us to visualise the still two dimensional experience of the flatlanders from our three dimensional perspective by making them similar to us in a very restricted way. The flatlanders themselves will not be aware that this involves a third dimension, and will interpret such objects as being made of a material having a peculiar and unexplained kind of transparency.

We must now begin to determine what the flatlanders can discover, experimentally, about the geometry of the surface they inhabit. The usual analysis of curved surfaces, using an embedding space, makes it clear that, at any point, P, on a smooth, 2-dimensional, curved surface, the surface in the immediate vicinity of the point, P, approximates to its tangent plane at that point. The smaller the

region considered the better is this approximation. That is to say, the smaller the region that is being examined the more accurately will measurements made within it approximate to corresponding measurements made within the tangent plane around the same point. This means that a surface geometry confined within a small region around the point, P, will approximate to the Euclidian geometry of the tangent plane, or will contain measurements that depart from it by only very small amounts. If the flatlanders have rulers less accurate than would be required to detect the errors caused by the curvature of the surface itself, they will be able to discover, experimentally, within such a small region, an apparently strictly Euclidian geometry. If they succeed in doing this, they will find, experimentally, however, that any investigations carried out within a larger region will not give geometric results that correspond to those within the much smaller region. This will be, for them, a puzzle they will have to solve, which they will do by investigating whether or not the departure of the larger scale geometry from that of the small region can be formally determined in some consistent way.

However, in order to experimentally discover a Euclidian geometry within a small region of the curved surface, the flatlanders will have to have discovered the local equivalent of the straight line. They will have to do this in spite of the fact that the line is curved and not really straight in the strict sense. So we must ask the question: how might they be able to do this? How, indeed, might the strictly correct straight line have been discovered initially, even in a Euclidian space?

One might answer immediately that it can be defined as the path involving the shortest distance between two points. This, however, appears tautological, since 'distance' is a concept defined in terms of the straight line, and depends on it, and cannot, therefore, be used to define the straight line before the straight line exists. That is to say, if the straight line doesn't yet exist, the paths connecting any two points whatsoever are all arbitrary, and an arbitrary path cannot be used to define a non-arbitrary concept of 'distance'. Thus, a comprehensive analysis of our problem leads us to the necessity to define how a straight line might come to be defined or discovered before any geometrical concepts whatsoever yet exist. This will be the task of the next section.

WHAT IS IMMEDIATELY DISCOVERABLE FROM AN INTRINSIC PERSPECTIVE?:

At first, as mentioned, the flatlanders initially have no geometrical concepts, no straight line, and thus no formal concept of 'distance' or 'direction'. They do, however, have primitive cutting tools. They have discovered, also, that, by sliding certain two dimensional objects over one another (which they can do in the very thin third dimension), and working around the edges with their primitive cutting tools, they can make identical copies of two dimensional objects. So one day, in this way, for amusement, a flatlander makes a large number of identical copies of some arbitrarily shaped two dimensional object. Having nothing else better to do with them, he lays them end to end between two fixed points in his two dimensional environment, along an arbitrary path and also randomly oriented relative to one another, and finds that, by varying the path, he can connect the two fixed points using different numbers of the arbitrary shapes.

He suddenly gains an intuition that there is some peculiar kind of meaning hidden somewhere in this discovery, which leads him to experiment more extensively with this phenomenon. Eventually he discovers that there is a unique path, and a particular relative orientation of the shaped objects, which allows him to use a minimum number of the shapes to connect together the two fixed points. He further makes the remarkable observation that this path is the same as that which the flatlanders would use to walk from the one fixed location to the other, in the particular case in which they walk directly towards the light coming to them from the location towards which they are walking.

Over a period of time, continuing to amuse himself experimenting with these observations, he discovers that the same path will be identified by the minimum number of shapes necessary to connect the one fixed point to the other, no matter what might be the actual size of the identical shapes used to carry out the experiment. He also discovers that the number of steps a flatlander needs to take to walk from one point to the other is also roughly a minimum along that same path. He further eventually discovers that the same results obtain for any other pairs of fixed points in his world.

It is to be noted, here, that the flatlanders have no conception of the geometrical significance of a local geometry compared to a large scale geometry, within their curved two dimensional world, and our experimenter makes no attempt to limit what we would call the distance apart of the various pairs of fixed points which he uses in his experiments. Nevertheless, he always gets the same results, whether the locations are what we would describe as close together or far apart.

I shall now show that the flatlander's experiments can be described in our mathematical terms, if the terms are initially given entirely non-mathematical meanings.

An arbitrary shape I shall label with the label ds.

This label has nothing to do with any concept of an element of 'distance'. It is merely the name of one of the arbitrary shapes the flatlander used for his experiments. Now I shall call the result of his process of counting the shapes Σds. His process of removing shapes, in changing from one path to another, thus causing him to count a reduced total number shapes, I shall refer to as δΣds, to mean the number of shapes he has removed in this operation. When he reaches the minimum number of shapes connecting the two locations, and finds he cannot remove any more shapes, if he wants the two locations to remain connected together, I shall refer to the removal of no shapes as δΣds = 0.

We now have the remarkable result that the non-mathematical flatlander's experiments (apart from the process of counting) can be described by a virtually non-mathematical version of Einstein's equation δΣds = 0, and that this description applies independently of whether the flatlanders two dimensional world is curved or not. This equation is therefore pre-mathematical and pre-geometrical and is the fundamental basis of all geometry, on which all geometry depends, including even the definition of the straight line.

If I call the unique path discovered by the flatlander the geodesic connecting his two locations, I can conclude that the geodesic is the fundamental and immediate intrinsic geometrical property of all spaces, curved or flat, and the straight line is only a special case of this, and not prior to, or more immediate than, any other geodesic.

This is established only by the experimental scenario described so that, if its validity is questioned, it can be confirmed by repeating experiments on a curved two-dimensional surface, equivalent to those carried out by the flatlander.

The consequence of all this is that the geodesics of a curved surface are no less immediate than straight lines, and can be assumed equally with them, and do not have to be derived from them. That is, we can begin the analysis of a curved manifold by assuming its geodesics in the same way we can begin the analysis of a flat space by assuming its straight lines. This is because the experiments can show that geodesics are no less immediately discoverable experimentally in a curved surface than are straight lines in a flat surface or space.

I shall introduce, here, for simplicity, a limitation within the flatlander's experiments, which occurs accidentally, and which he does not deliberately choose. That is, the regions within which he carries out his experiments are never large enough for him to discover more than one geodesic connecting any two points, such as, for example, the two geodesics connecting any two points on a great circle of a spherical surface.

THE FLATLANDERS FIRST GEOMETRICAL EXPERIMENT:

Having established the geodesic as the pre-mathematical fundamental basis of all geometry, we can proceed to connect the pre-mathematical version of Einstein's geodesic equation with its normal mathematical version. I shall not continue to follow the flatlanders gradual experimental

development of a strictly mathematical geometry, which would involve a long story, including possibly a good deal of irrelevant collateral diversions. Instead, relying on what we already know, mathematically, I shall leap ahead to simply examine the results the flatlanders would eventually discover.

THE GEODESIC PRINCIPLE, AND THE FUNDAMENTAL PROPERTIES OF GEODESICS:

The flatlanders have established for us the initial non-mathematical version of the geodesic equation:

δΣds = 0

Now, if their experiment is carried out with a third, fourth, or more set of shapes, reducing the number joining P and Q, as before, each time. We know that a practical experiment would produce the same minimum number of shapes, n, each time and, furthermore, each final set of shapes will always perfectly coincide with the shapes in the path formed by those of all of the other experiments. This establishes the unique nature of the geodesic path joining P and Q,

To make this even clearer, let us set up a point Q’, very close to Q, such that the same number of shapes, n, with the same points of contact between the individual shapes, will only just reach Q‘. It will be found that, as with Q, no other path formed by the shapes, and no other rotational orientation of the individual shapes, will allow P to be joined to Q’. Furthermore, it will be found that if all the shapes joining P to Q are used to join P to Q’, by moving them from the path PQ to the path PQ’, every one of the shapes will have to be moved onto the new path PQ’, and not only some of them. That is, the paths nowhere perfectly share any portion of their paths in common, which is a concept not contradicted by the fact that the shapes will overlap. The point being made is that none of the shapes forming one path will perfectly coincide with any of the shapes forming the other. This will be true of all geodesic paths from P to any other point in the space that is not on the path between P and Q, or that does not incorporate the whole of the path PQ

We can thus declare two fundamental properties of

geodesic paths, created from any point, P:

1) A geodesic path is a unique path defined by a unique arrangement of the minimum number of shapes necessary to join any point P with any other point Q, and

2) Any geodesic path originating at a point, P, is unique and distinct in its entirety, and in all its parts, from every other geodesic path originating at P.

These are the fundamental properties of geodesics, immediately observed, or discovered by experiment, and are not derived from any more fundamental principle. Since we have as yet no concept of length or distance, and no concept of any kind of geometry, the two properties of geodesics are prior to all measurement and all geometric truths, apart from themselves, and are not dependent on them or derived from them. On the contrary, the whole body of geometric truths of all kinds, including the whole of Euclidian geometry, originate in these two properties of geodesics, which apply equally and without distinction to all geodesics. I therefore repeat, and reemphasise, that this means that a geodesic of a curved manifold is as immediate and fundamental a connection between one point an another as is the straight line in Euclidian space, and is not generated by, or derived from, anything prior to it.

The two fundamental properties of geodesics can be used to immediately generate useful concepts, but first let us refine the geodesic thus far constructed to make it more suitable to support such concepts with greater clarity.

DEFINING THE TWO FUNDAMENTAL PROPERTIES OF GEODESICS:

Let the shapes represented by ds now be made so small that they are almost invisible, but still sufficient to carry out the procedure involved in creating a geodesic. The appearance of the set of shapes joining P and Q will now have a character approximating what we recognise as a very thin, or one dimensional, line joining P and Q.

Now let ds be taken to represent a small subset of the set of shapes, instead of only a single shape, and let it contain m shapes, where m << n, n being the total number of shapes along the whole geodesic PQ, as before. It will be seen immediately that the shape referred to by ds is very much like the shape of the line joining P and Q as a whole, i.e. it has the

appearance of a small line segment. Furthermore, since it coincides with the geodesic path joining P and Q, and forms part of it, ds must itself contain the minimum number of shapes that can form its own part of the larger path; that is to say ds, as a path segment, is itself a geodesic. Thus, an important feature of the geodesic PQ, and consequently of any geodesic, is that the path by which it connects P with any other point, O, along it between P and Q also contains a minimum number of shapes, and is also a geodesic connecting P with O. By a similar argument, any intermediate portion, ON, of a geodesic path, joining points O and N on it, is also a geodesic connecting O to N.

CONVERTING THE PATH TO A LINE:

The above argument establishes that any portion, ON, of a geodesic path is also a geodesic joining O and N. Let the segment, ON, be now taken to be so small that it exists within a region of the surface around the point O which approximates to the surface tangent plane at O. That is to say,

within this region, the surface geometry would approximate to Euclidian geometry and therefore the geodesic segment, ON, as a portion of the large scale surface geodesic, approximates to a straight line within the surface.

THE SPECIAL SIGNIFICANCE OF A VERY SMALL GEODESIC SEGMENT:

Let us now arrange that a second set of very small, almost-invisible shapes form another line joining P and Q, and let it also be a geodesic, which will therefore lie alongside the first and in contact with it all along its length. This assumes that both lines are so narrow that together they can effectively be taken to form the same single geodesic path, such that the distinction between the two lines is, in reality, only a construct of the mind. Now we may mentally transfer ds to the second line and, in addition, we may successively redefine the location of ds so as to make it slide along the new path. In this case it will at all times be in contact in all its constituent shapes

with corresponding constituent shapes in the first path, since both paths are effectively identical. That is, the shapes will perfectly coincide with one another. Let us call this principle of keeping the segment ds in contact with the geodesic path as keeping it ’parallel’ to the path. By means of this procedure, the motion of ds along the geodesic can be referred to as a 'parallel transport' along it, since it remains parallel at all times. This procedure can be used for the dynamic generation of geodesics, as described further on. But first we must consider some useful consequences that flow from the two fundamental properties of geodesics.

THE PRIMITIVE CONCEPT OF PARALLELISM AND PARALLEL TRANSPORT:

Let us now return to the definition of 'parallel transport', which involved transporting a segment, ds, along a second geodesic that was effectively identical to the first, and thus 'parallel' with it. If ds is very small, which is to say, if its 'length', which we have now defined, is very small, ds will occupy a local region of the surface, within which the surface geometry is effectively Euclidian, so that ds will effectively be a straight line segment. It will therefore be parallel transported along local, straight line geodesic segments of the global geodesic, since every segment of a geodesic, however small, is itself necessarily also a geodesic, as argued before. The transport of ds locally, as a straight line segment, will therefore correspond to the notion of parallel as it exists within a Euclidian geometry. This inevitably means that, if a straight line segment is parallel transported locally, in a Euclidian sense, within a

curved surface, and this process is continued beyond the initial local region, it will enter another local region that overlaps with it, within which it will again continue to be parallel transported in a Euclidian sense, even though the local regions involved are not locally Euclidian when taken together. In other words, if a small, straight line geodesic segment is parallel transported in a Euclidian sense, it will progressively and dynamically generate a global, non-Euclidian geodesic across a curved surface. Our flatlanders could, in fact, experimentally use this method to dynamically generate the geodesics of the surface, without having to use only the geodesic equation as the basis of doing so. This justifies regarding curved geodesics, in general, as auto-parallel, in the same way that a straight line is auto-parallel within a flat surface.

DYNAMIC GENERATION OF A GEODESIC BY PARALLEL TRANSPORT:

Up to this point the fundamental geodesic equation has not yet acquired its usual mathematical form. Since, however, we are now able to identify ds as a segment having the significance of a measurement of ‘length’, or distance, and our geodesic equation, which originated merely as a counting of a number of shapes, has now acquired its usual mathematical significance. It now appears, in terms of the summation of segments of the measurement of distance, to give an overall measurement of distance, as a specification, and definition, of the ‘shortest’ path joining P and Q. We remember, of course, that our experiment has excluded cases such as that in which we can reach Q via geodesic paths in opposite directions along the great circle of a sphere.

With ds being used to signify line segments of infinitesimal length, the equation δΣds = 0 can be written in the usual form

δds = 0

This mathematical version of the equation is thus the fundamental mathematical equation of all geometry, and is prior to all further geometrical equations, concepts, and relationships of every kind. It applies equally to flat or curved spaces and is equally fundamental to them all.

The whole of geometry likewise depends on the two properties of geodesics, and could not exist without them. They must be seen to have a fundamentally immediate, experimental basis, for the reason that they could originally have had no other. Thus, any geometrical conclusions, in any manifold, that are derived from an assumption of the foregoing properties of geodesics will, if they are true, be confirmed by any experimental test of them.

THE MATHEMATICAL VERSION OF THE GEODESIC EQUATION:

We have now reached the point where we must consider the question whether or not the flatlanders will be able to discover and measure the curvature of their world. If they cannot, it will have to be concluded that a completely intrinsic analysis of a curved manifold is not possible.

We have already said enough to recognise that the flatlanders will eventually be able to discover the locally Euclidian geometry of any small region of their two dimensional world. They will thus be able to draw arcs of circles at different radii, and will have discovered the equation X = rθ, where X is the arc length, drawn through the angle θ, in radians, at a radial distance r. We may suppose that the flatlanders will also have established, by experiment, that, if the radius used to draw the arc becomes too large, this equation will cease to be true, and that the arc length X will become progressively less than the equation would predict, as the radius is increased.

Let us suppose that eventually one of the flatlanders will try to discover whether or not this occurs in any regular and predictable manner. Let us say that he rewrites the equation in the form X = krθ, with k being some fractional value, as a function of the arc radius, to make the equation correspond to experimental results.

We can suppose that the flatlanders, who now possess Euclidian geometry, will have Sine and Cosine tables, etc. I will now make the supposition that, for some reason I don't know, some flatlander also created a table of values of (Sinθ)/θ, and that our flatlander, experimenting with circular arcs, discovers that the values of k in his equation correspond to those of the (Sinθ)/θ table.

He now feels certain that he is on the verge of discovering some property of his world which causes the arcs of circles to be modified in some specific way. He eventually notices that his discovery relates to the relative values of the circular arc to the partial chord shown below, so that the actual arc within his world is being drawn as if the radius is really rSinθ

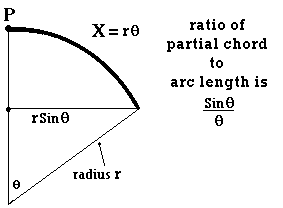
This suggests that the surface radius used to draw the arc is not the 'real' radius that is actually drawing the arc, as shown below.

Our flatlander puzzles over this for a considerable time, in an attempt to discover where the 'real' radius of the arc might actually be, and where the fulcrum of rotation of the real radius, shown as P', might be. He cannot conceive any possible location for it, within his visible world, that makes any sense in terms of providing a meaningful explanation as to why the value of k has to have the form Sinθ/θ. This is made worse by the fact that the value of θ does not appear to be related to the angle through which the radius of the arc is drawn on the surface. That is, if the surface radius of the arc, r, draws an arc through an angle θ, k will adopt values of another angle Sinφ/φ, which will depend on r, but will be unaffected by, and unrelated to, the value of the angle θ. Our flatlander thus also cannot make sense of the angle φ, or discover where it might be located.

But suddenly, one day, his failures lead him to a flash of intuition, that the 'real' radius that is drawing the arc may, in fact, not be within his world at all but, rather, somehow outside of it altogether. He immediately senses the significance of this consideration and, knowing that he inhabits a two dimensional world, is led to suppose that, in fact, he may have to conclude that he is inhabiting a three dimensional world, from within which he can see in only two dimensions, with the third being inaccessible to him. He then gradually realises that, in this three dimensional reality, his world must be actually curved, and that the fulcrum, P', of the real radius that draws the arc is located somewhere

outside his world, in the manner shown below. He thus also realises that the angle φ must be related to a radius R, completely separate from the surface radius r, which is actually curved, with R being the radius of its curvature.

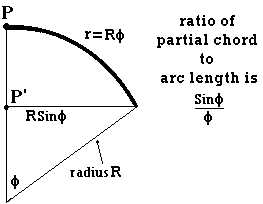
Our flatlander then concludes that the complete explanation of his experimental observations is accounted for by a curved two dimensional surface segment, in the manner shown below, although he has as much difficulty visualising this in three dimensions as we have in attempting to visualise what a four dimensional object might look like.

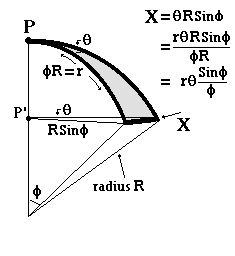
He now knows why the value of k has to have the form Sinφ/φ and is, moreover, able to determine the curvature of the surface, since both r and θ are measured on the surface, and φ can be calculated from his tables. He can thus obtain the value of R from the equation r = Rφ

This result, of course, depends on a supposition that the value of R does not change along the length of r. We must therefore ask whether or not the flatlanders can determine whether or not the value of R is constant?

If they examine the total differential of X, in which both r and R are allowed to change, they will obtain

dX = (δX/δr)dr + (δX/δR)dR

If the radius R does not change as the length of r is increased, then

dX = (δX/δr)dr, since dR is zero
= θ(Sinφ/φ)dr

If the total value, dX, begins to depart from being directly proportional to dr, we know that the curvature is beginning to change with increasing values of r.

If R is not constant, the flatlanders can try dividing the length r into two segments of value r/2 each, and separately examine the curvatures of the two halves, as shown below (where I still call each half r, for convenience)

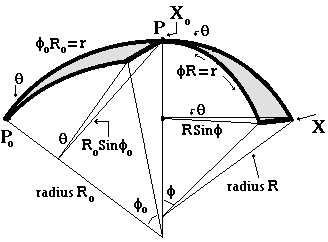
In this way they should be able to determine the change in the radius of curvature R along the geodesic r

If the value of the angle θ is small, the flatlanders will be able to calculate the radius of curvature of their world in roughly one direction, and, in a similar manner, can go on to build up a profile of the curvature of their world in all other directions.

CAN THE FLATLANDERS DISCOVER THE CURVATURE OF THEIR WORLD?:

Since the flatlanders have been able to obtain the value of the curvature of their two dimensional world, they have direct theoretical access to its three dimensional Euclidian embedding space. They will thus be able to determine the first and second fundamental forms applicable to their surface. They can also construct a geodesic curvilinear coordinate system on their surface, which is the natural coordinate system of a curved space, just as it is in a Euclidian space. We would not construct a non-geodesic coordinate system in a Euclidian space, unless for a very special, extraordinary reason.

The flatlanders do not require a Riemannian analysis of their world, and do not need an Affine connection. The geodesic is the immediate, fundamental connection in any space, and does not have to be derived or

determined by any equation.

It is not my intention to proceed with a further analysis of the geodesic geometry of curved spaces, since I have achieved the purpose of establishing the fundamental nature of the geodesic, the fundamental equality of all geodesics, and the fact that the geodesics of a curved space do not have to be derived. There are any number of mathematicians who can easily develop the consequences of this fundamental starting point. Instead, it will be much more fruitful to examine (in part II) the way in which the fundamental geodesic principle implies that Nature, and the laws of Physics must relate to, and must make use of, geodesics in any space, flat or curved.

CONCLUSION - THE GEODESIC AS THE FUNDAMENTAL CONNECTION IN ALL SPACES:

Part II (Page 2) - Hamilton's Principle of Least Action

© Alen, March 2007; update Dec 2010.
June 2019 - re-engineered to display properly on Chrome and Firefox.
alen.1@bigpond.com

Material on this page may be reproduced
for personal use only.