
EINSTEIN'S DERIVATION
OF THE TRANSFORMATION EQUATIONS
IN SPECIAL RELATIVITY
INTRODUCTION.
Anyone who reads Einstein's derivation of the transformation equations of Special Relativity in his 1905 paper may find it somewhat cryptic and unclear, especially on a first acquaintance, since he does not include all the intermediate mathematical steps in the argument. No doubt he could have supposed that his peers of the time would easily have been able to fill in the missing steps for themselves.
Now, however, Special Relativity has a much wider audience, some of whom are subjecting it to doubts and controversy, or even, perhaps, saying that Einstein fudged some steps in the argument.
Since the cryptic nature of the presentation makes it difficult for someone trying to read it for the first time, it seemed to me that it might be useful to have Einstein's 1905 argument, with relevant illustrations added, and with the missing mathematical steps filled in. This is what I have attempted to do in what follows. It deals, of course, only with the 'kinematical part' of Einstein's paper
The derivation is grounded in the two postulates of Special Relativity, the first being that all inertial reference frames provide equally valid viewpoints from which to describe events in general, in the sense that no inertial reference frame can be given a special status in preference to any other, and the second being that the velocity of light is the same if measured within any inertial frame, independently of the reference frame in which the light was emitted. The validity of the transformation equations that result from the derivation depend on the correctness of these postulates, which are not proven by argument, but depend entirely on accepted experimental verification for their credibility.
The 1905 paper deals with the case of two inertial reference frames in constant relative motion. We rigidly connect ourselves to one of the frames so that
it is not moving relative to us, and so that we can thus call it the 'stationary' frame. The other frame then becomes the 'moving' frame. We could connect ourselves to either frame, or neither, in which case both frames would be moving relative to us. It is simpler, however, to arrange for one of the frames to be stationary relative to ourselves.
Einstein starts off with a context that is illustrated in the diagrams below. The event whose coordinates are to be considered is event B, and this is described in the moving frame by coordinates of the type, ξ,η,ζ,τ, and in the stationary frame by coordinates of the type, x,y,z,t. Einstein sets out to derive a relationship between these two sets of coordinates, by which one set can be obtained from the other. This is expressed in a general way as one set being a function of the other, or forming a 'basis' for the other. So we will be dealing with ξ(x,y,z,t), η(x,y,z,t), ζ(x,y,z,t), and τ(x,y,z,t) as the general expression of the relationship. Einstein begins with the derivation of τ(x,y,z,t).
There are, however, two versions of this general transformation: a transformation of a first kind, in which x,y,z,t are coordinate values referred to the origin of the stationary frame, as in figure 2, and a transformation of a second kind, in which they are referred to the origin of the moving frame, but remain stationary frame measurements, as in figure 3. In the two kinds of transformations the values for both τ(x,y,z,t) and t are the same. Only values of the x coordinate are different. The desired, final equations that are to be derived are the transformation equations of the first kind. Einstein uses both kinds of transformations in his paper, in respect of the values of τ(x,y,z,t), for which they are equivalent, but does not overtly discuss the difference between them.

Einstein refers to the velocity of light being c-v or c+v, rather than c, in the moving frame, from the perspective of the stationary observer. The existence of two distances and two times as, ξ and x, and τ and t, provides for four possible values that can be assigned as a 'velocity' of light: x/t, ξ/τ, x/τ, and ξ/t. The principle of the constancy of the velocity of light refers only to this velocity being measured by the distance and the clock being in the same frame, and not by distance in one frame and the clock in the other. Thus, only x/t and ξ/τ must have the value c. When referring to a velocity of, for example, c-v, Einstein is using the form ξ/t, using distance in the moving frame and a clock in the stationary frame. The value obtained is not actually ξ/t but, rather, X/t, where X is the measured, foreshortened value of ξ that can be obtained by the stationary observer.
A form such as X/t, where X is a distance within the moving frame, and moving with it, represents the stationary observer's attempt to see how the light, emitted in the moving frame, is travelling within the moving frame, rather than within his own stationary frame. This is illustrated in figure 3. That is, he tries to eliminate the relative motion from his viewpoint in order to see what the moving observer sees, but necessarily uses stationary frame calculations. But this causes him to interpret light as travelling within the moving frame at values of velocity other than c, ie (c-v), or (c+v). The postulates of relativity, however, declare that the moving observer does not see the light moving in accordance with these values, and the coordinate values of events therefore have to be transformed to allow the stationary observer to understand the values the moving observer would obtain. This is achieved by the transformation equations of the second kind. Einstein begins by constructing these equations and then uses them to obtain the desired transformation equations of the first kind. As indicated previously, the viewpoint on the basis of which the transformation equations of the second kind are obtained involves a relationship of figures 1 and 3, rather than figures 1 and 2.
In figure 1, we can see that, since, within the moving frame, for the moving observer, the frame is the same as a stationary frame, within which the rod is also stationary, the light takes equal times to go in both directions, so that the time at event B must be half way between the times at events A and C on a moving frame clock, which can be expressed as τ - τ0 = τ1 - τ or τ0 + τ1 = 2τ, which means 1/2(τ0 + τ1) = τ. The corresponding times for the stationary observer, as seen in figure 3, are t0, t0 + X/(c-v), and t0 + X/(c-v) + X/(c+v), where the capital X refers to the measured value of the length of the moving rod as would be obtained by the stationary observer. It can be seen immediately that, for this original stationary observer, who sees the light trajectory according to figure 2, in his own frame, the time at event B is not half way between the times at A and C, on his stationary clock. This makes it clear that the times on stationary and moving clocks cannot correspond.
For the expression 1/2(τ0 + τ1) = τ, as a function of the stationary coordinate values in figure 3, we have:
1/2{τ0(0,0,0,t0) + τ1(0,0,0,t0 + X/(c-v) + X/(c+v))}
= τ(X,0,0,t0 + X/(c-v))
if X is sufficiently small, this has the differential form
1/2{τ0(0,0,0,t0) + τ1(0,0,0,t0 +dt1)}
= τ(dx,0,0,t0 +dt),
or, 1/2{τ0(0,0,0,t0) + (τ0+dτ1)(0,0,0,t0 +dt1)}
= (τ0+dτ)(dx,0,0,t0 +dt). . . . . . . . . .(1)
with dt1 = X/(c-v) + X/(c+v), and dt = X/(c-v),
writing dx in the form X, to correspond with the illustrations.
Einstein proceeds to carry out the derivation using differential equations, rather than macroscopic equations, and uses a principle of linearity to convert to macroscopic equations, which I shall do at the end of the derivation.
Thus, using the well known partial differential expression for the transformation of the total
differential, we can say, in general:
dτ = (δτ/δx)dx + (δτ/δy)dy + (δτ/δz)dz + (δτ/δt)dt
and this can be applied separately to each term in the previous differential equation (1), so as to get a differential transformation for each value of dτ in that equation. The values with subscripts correspond to those shown in the illustrations above. All differential values are expressly indicated, so the results can be simply written down immediately.
For the first term, on the LHS of equation (1), we are at the start, at event A, in figures 1 and 3, where there are as yet no dτ or dt, or other differential values, so it can be ignored. In the second term, we are back at the start spatially, at event C, where dx = 0, and only times τ and t are different, so, applying the above expression for the total differential, we have
dτ1 = (δτ/δt)dt1. . . . . . . . . . . . . . . . . . . . . . .(2)
with the other terms zero.
At event C, we have dt 1= X/(c-v) + X/(c+v), and thus
dτ1 = (δτ/δt)( X/(c-v) + X/(c+v)). . . . .(2a)
For the right hand side of equation (1), at event B, we have values for dτ and both dx and dt, and so, here, dτ, will be
dτ = (δτ/δx)dx + (δτ/δt)dt. . . . . . . . . . . .(3)
with the other terms zero
here, dt = X/(c-v), and dx = X so we have:
dτ = (δτ/δx)X + (δτ/δt) X/(c-v). . . . . (3a)
It is worth examining more closely the nature of the term (δτ/δx)X, and ask what does δτ/δx mean? Since it is a partial derivative, it is a value taken when τ varies only in the x direction, and not any other, also excluding the time direction. The variation of τ along the x direction, without varying the time, can therefore refer only to the rate of change of the nonsimultaneity of readings on an array of clocks along the x direction, which is the axis in the direction of the relative motion. That is, the stationary observer will see an array of moving clocks, fixed to this moving axis, showing times which are different to one another.
Since the differential equation has been written in the form
1/2(τ0 + (τ0+dτ1)) = τ0 + dτ. . . . . . . . . (4)
we can eliminate τ0, and get the differential equation
1/2 dτ1 = dτ. . . . . . . . . . . . . . . . . . . . . . (4a)
and, substituting values obtained above for dτ1 and dτ, we have
1/2(δτ/δt)( X/(c-v) + X/(c+v))
= (δτ/δx)X + (δτ/δt) X/(c-v)
(δτ/δt)cX/(c2-v2) = (δτ/δx)X + (δτ/δt)X/(c-v)
= (δτ/δx)X + (δτ/δt)X(c+v)/(c2-v2)
From which
(δτ/δx)X = (δτ/δt)(-vX/(c2-v2)). . . . . . . (4b)
Putting this into the equation for dτ, which refers to the time existing at event B, we have*
dτ= (δτ/δt)(-vX/(c2-v2)) + (δτ/δt)(X/(c-v))
= (δτ/δt)(-vX/(c2-v2)) + (δτ/δt)(X(c+v)/(c2-v2))
dτ = (δτ/δt)(cX/(c2-v2)). . . . . . . . . . . . . . . . . . (5)
Now we can say, putting γ = 1/(1-v2/c2)1/2
cdτ = dξ = (δτ/δt)(c2/(c2-v2))X = (δτ/δt)γ2X
and
dτ = (δτ/δt)(c2/(c2-v2))X = (δτ/δt)γ2X/c
which are the first two transformation equations of the second kind.
* Here I take a different route to the following one taken by Einstein:
I substitute the result indicated by equation 4b into dτ as it appears in equation 3a, whereas Einstein substitutes it into dτ as it appears in equation 3, although, as usual, he doesn't fully describe the steps he is taking
The expression for the total differential, using Einstein's notation, gives:
dτ = (δτ/δx')dx' + (δτ/δy)dy + (δτ/δz)dz + (δτ/δt)dt
with the two middle rhs terms zero, we get
dτ = (δτ/δx')dx' + (δτ/δt)dt. . . . . . . . (e1)
from δτ/δx' + (v/(c2 - v2))(δτ/δt) = 0 we get
δτ/δx' = (-v/(c2 - v2))(δτ/δt). . . . . . . . (e2)
so, substituting this in the rhs for δτ/δx', in equation e1, equation e1 becomes
dτ = (-v/(c2 - v2))(δτ/δt)dx' + (δτ/δt)dt
dτ = (δτ/δt)(dt - (v/(c2 - v2))dx'). . . . . (e3)
Einstein wrote (δτ/δt) as an unknown function a, without saying what a is, or where it occurs in the derivation, or where he got it from, which made it look as if he simply took it out of thin air for some unknown reason. This makes the equation to be misleading and confusing.
In any case, we have
dτ = a(dt - (v/(c2 - v2))dx'). . . . . (e3a)
The fact that the equation is linear means that you can translate the differential equation directly to a macroscopic form, so we get
τ = a(t - (v/(c2 - v2))x'). . . . . (e4)
If we substitute for x' in this equation, where
x' = (c-v)t, and x = ct
we get
τ = a(t(c2 -v2) - vx + v2t)/(c2 -v2). . . . (e4a)
which leads to
τ = aβ2(t - vx/c2). . . . . . . . . . . (e5)
where
β = 1/(1- v2/c2)1/2
Einstein said earlier on, when first introducing a, that a = φ(v) but, because he wants to write the equation η = φ(v)y, with a similar equation for z, he now changes φ(v) to φ(v) = aβ instead of a. Again he confuses the reader by making no reference to the fact of this change. So he gets the equation for τ as
τ = φ(v)β(t - vx/c2). . . . . . . . . . . (e6)
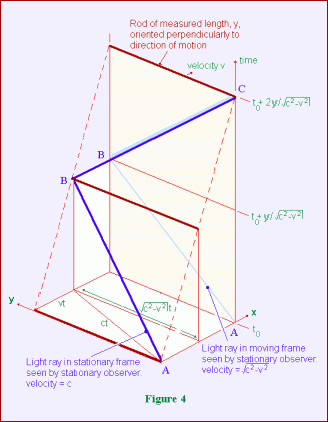
Einstein now considers the case where we have a light ray to move along the y axis, transverse to the direction of motion, instead of the x axis, so we must have another transformation equation of the second kind. The diagram in figure 4, on the, left illustrates the case where the light ray moves transversely to the direction of motion of the rod, and the shaded panel indicates the parameters used to set up the equation below. The shaded panel represents the stationary observer's attempt to interpret what the moving observer sees, using stationary frame measurements, and is a transverse case version of what is illustrated in figure 3. It does not represent the moving observer's own observations, which would be identical to figure1, since there is no distinction between the results of transverse observations and observations in the direction of motion within the moving frame. This diagram gives the following equations, which I put immediately in the form of differentials, by assuming y is very small:
1/2{τ0(0,0,0,t0) + τ1(0,0,0,t0+2dy/(c2-v2)1/2)}
= τ(0,dy,0,t0+dy/(c2-v2)1/2)
. . . . . . . . . . . . . (6)
or,
1/2{τ0(0,0,0,t0) + (τ0+dτ1)(0,0,0,t0+2dy/(c2-v2)1/2)}
= (τ0+dτ)(0,dy,0,t0+dy/(c2-v2)1/2). . . . . . . (6a)
All the subscripts have the same relationship to one another as before, but now refer to a corresponding arrangement of events in the transverse case. Applying the equation for the total differential, as previously, to dτ1 and dτ, each being regarded as a total differential, we get the equations
dτ1 = (δτ/δt)2dy/(c2-v2)1/2. . . . . . . . . . . . . . (7)
dτ = (δτ/δy)dy + (δτ/δt)dy/(c2-v2)1/2. . . (7a)
and with, as before
1/2 dτ1 = dτ
we get the equation
(δτ/δt)dy/(c2-v2)1/2
= (δτ/δy)dy + (δτ/δt)dy/(c2-v2)1/2. . . . . . . (8)
so we must have δτ/δy = 0 and, by a similar argument, δτ/δz = 0 (which show that there is no non-simultaneity effect within any array of clocks fixed to a moving plane at right angles to the direction of motion)
thus
dτ = (δτ/δt)dt = (δτ/δt)dy/(c2-v2)1/2
or
cdτ = dη = (δτ/δt)dy/(1-v2/c2)1/2 . . . . . . . (9)
and, by a similar argument for the z axis
cdτ = dζ = (δτ/δt)dz/(1-v2/c2)1/2. . . . . . . (9a)
Einstein has (δτ/δt)/(1-v2/c2)1/2 as an unspecified function φ(v), so that the transformation equations of the second kind are
dξ = φ(v)γX
dτ = φ(v)γX/c
dη = φ(v)dy
dζ = φ(v)dz
Einstein now has to obtain the value of φ(v). First he uses a double application of the transformation equations so that, for example, we transform dy => dη => dy, and similarly with the other coordinates, and then argues that we must have φ(v)φ(-v) = 1, since transforming forward, and then back again must give us back the original values.
He then argues that we have dη/φ(v) = dy, and neither dη nor dy change with a change in the direction of motion along the x coordinate, so we must have dη/φ(-v) = dy, if the direction of the velocity is reversed. Since, however, all inertial frames are equivalent, the value obtained for φ(-v) here must be symmetrically the same as that obtained already, by viewing the velocity as -v from the perspective of the other frame. So dη/φ(v) = dη/φ(-v) must be true, which means φ(v) = φ(-v) = 1
Since we have, above
(δτ/δt)/(1-v2/c2)1/2 = φ(v) = 1
Therefore
δτ/δt = (1-v2/c2)1/2 = 1/γ
This shows that δτ/δt depends only on velocity, v, so that the transformation equations must be linear at constant velocity, allowing the differential transformation equations to be written as macroscopic equations.
To get the desired, macroscopic transformation equations of the first kind, we must use coordinate values in figure 2 and, for simplicity, set τ0 = t0 = 0. We may note that event B, which is at coordinate value X in figure 3, is at some coordinate value x in figure 2 and, since the length of the moving rod is X = (x-vdt), which gives X = (x-vt), in the macroscopic version of the equation, as indicated in figure 2, we can get equations in terms of x by substituting for X. In the first transformation equation we can use the form (x-vt). In the second equation, since we have x = ct, and also vt = vx/c, we will get X/c =( t - vx/c2). Thus, if we put φ(v) = 1, the macroscopic transformation equations of the first kind are:
ξ = γ(x-vt)
τ = γ(t-vx/c2)
η = y
ζ = z
Notes on the Inverse Transformation
While the above page contains nothing regarding Special Relativity and the transformation equations that is unorthodox, the following links connect to pages that do contain an unorthodox interpretation of the transformation equations. This is because I have been forced to the realisation (as demonstrated in these links) that, although the Minkowski equation is mathematically valid, it can be proven that the Minkowski metric cannot
represent a really existing spacetime.
In this context I will add that I have never attempted, nor will I ever attempt, to submit anything of mine to any peer review journal. If you want to know the reason for this you will find the answer in the page entitled Orthodoxy in Science, unless you find the title of the page alone to be a sufficient answer in itself.
© Alen, March 2007; update Dec 2010; Feb 2016
alen.1@bigpond.com
Material on this page may be reproduced
for personal use only.