
THE INVERSE TRANSFORMATION.
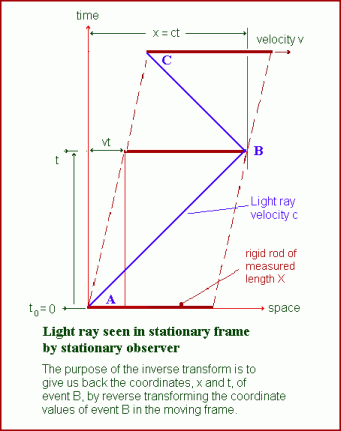
In order to get the inverse transformation, we transfer ourselves into the moving frame and, from there, must find transformation equations that will convert the moving frame coordinate values, already obtained by means of the forward transformation,
back into the original stationary frame coordinate values, x and t, associated with event B, as shown in the above illustration from figure 2 on the original page. The following illustration shows what we see on looking back into the original stationary frame.
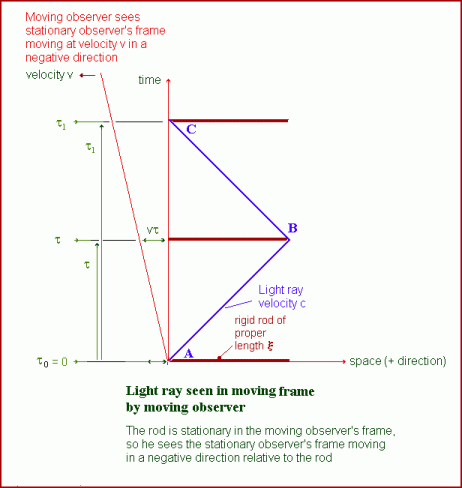
This viewpoint does not really help us to derive an inverse transformation, since we are now in the frame of the rod, which is stationary relative to us. What we can do, however, is calculate an inverse transformation from the already existing transformation equations of the second kind, as follows (setting φ(-v) = 1):
ξ = γX = γ(c-v)t
vτ = γvX/c = γ((c-v)/c)vt
adding these together, we get
ξ + vτ = 1/γct = 1/γx
thus
x = γ(ξ + vτ)
and
t = x/c = γ(ξ/c + vτ/c) = γ(τ + vξ/c2)
thus, the inverse transformation equations are
x =γ(ξ + vτ)
t = γ(τ + vξ/c2)
y = η
z = ζ
These equations enable us to set up an illustration indicating a method whereby these inverse equations could be derived directly, in the same way as the original equations. This illustration is shown below
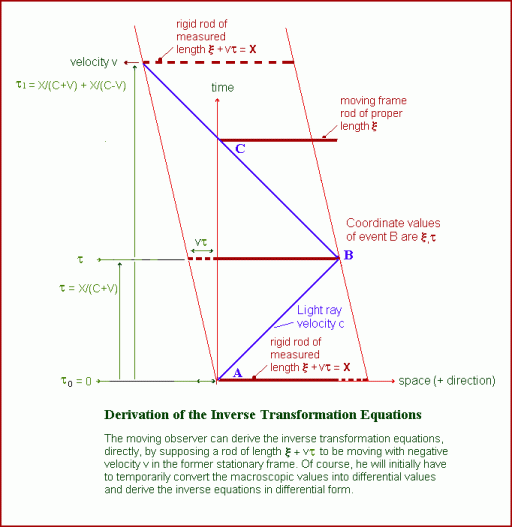
The above diagram is similar to the former diagram in figure 2 on the previous page, except that the velocity is in the negative direction, and the length of the rod is not the same. The length indicated here is a measured, foreshortened length, as would be obtained by the moving observer, now acting as a stationary observer. He imagines the rod, as shown, moving with the former stationary frame and, using his own coordinate values, he can derive the inverse
equations. In spite of the difference caused by the reversal of the velocity, the differential transformation equations of the second kind, using the value X, as shown, will have the same form as before, which you can easily prove by going through the same steps as before. The different form of the inverse equations appears when substituting for X, to get the final equations.
© Alen, March 2007.
alen@alenspage.net
Material on this page may be reproduced
for personal use only.