A RE-EXAMINATION OF BELL'S SPACESHIP PARADOX

The purpose of the following page is to re-examine the special relativistic Bell's Spaceship Paradox by proposing a method of what I call a spacelike observation of events in order to make a distinction between this and what I shall call a lightlike observation of the same events and then show that these two methods of observation of the same events produce results that do not agree with one another.

The thought experiment used here to make the comparison between the two methods of observation is essentially identical to that which is involved in Bell's Spaceship Paradox, and the argument is intended to show that the spaceship paradox has never been given a satisfactory answer.

INTRODUCTION:

The Concept of a Spacelike
Comparison of Events.

Simultaneous events, separated by a spatial distance, can be referred to as spacelike separated, since they cannot be connected by a light signal travelling between them, and cannot be observed simultaneously, since each will have ceased to exist when the light from the other arrives. It is thus impossible to directly compare such events as they occur.

Such spacelike separated events can, however, be simultaneously, but separately, observed, as they occur, if they each have their own local observer, the acts of observation of such observers being obviously spacelike separated in the same manner as the events they observe. It follows that, if each of two such observers, who are not in relative motion, has a clock that is synchronised with an identical clock in the possession of his fellow observer, a basis exists for what could be called a 'spacelike comparison' of the events they observe.

What this means is that each of the observers makes a permanent record of the data from the event he observes, and links this data with the time shown on his clock. From this it follows that a later comparison of the data records of the two spacelike separated events, which are linked by the fact that the clock times of the two separate observers were simultaneous, can show what features of the events were also simultaneous.

The conclusions of such a comparison are exactly the same as they would be if it were possible for an observer to travel from one event to the other, and back, at infinite velocity, as they occurred.

The Concept of a Lightlike
Comparison of Events.

The concept of a lightlike comparison of events is based on the fact that a single, local observer, located at one event, can directly gather data from two simultaneous, spacelike separated events, if he can arrange to receive light signals from the remote event.

He will not, of course, receive data from such events, which are simultaneous in his own frame, in a simultaneous manner, and will have to allow for the different times taken by light signals to reach him from the different events. To calculate this time, he can use light signals sent out by himself, and reflected back to him by the event he wishes to examine. This allows him to calculate that his light signal encountered its target event at a time = 1/2 the time taken for the light to make the round trip.

With such allowances being made, he can gather data from both events, and thus create a basis for a comparison, as in the previous case involving what I called the spacelike comparison of events. Although the comparison is made in the same manner, using recorded data, in this case the comparison does not similarly reflect the manner in which the data was actually collected.

I call this a 'lightlike comparison' of spacelike separated events because the observer has a lightlike relationship with the data gathered at the remote event, though not with the event itself. This is distinct from the previous case in which the data is gathered, in a spacelike manner, by two separate observers localised at the two events.

AN EXPERIMENT THAT IS LOCALLY SELF-CONTAINED:

This is a description of the experimental setup to be used in the argument further on.

The illustration shows a coil-and-magnet experiment, set in motion by the power pack mounted on the coil. Everything else in the illustration has to do with data collection by the local observer. The coil-and-magnet thus constitutes a completely self-contained system, independent of the observer, and everything else in the observer's inertial frame of reference. Initially, the coil-and-magnet are stationary and, therefore, start off in the observer's inertial reference frame.

The cause of the mutual accelerations of the coil and magnet is entirely contained within the coil-and-magnet system itself. This acceleration is switched off before the observer's clock time is defined as t = 0 and, therefore, at this time, the magnet has a constant velocity relative to the observer, and occupies its own inertial frame of reference.

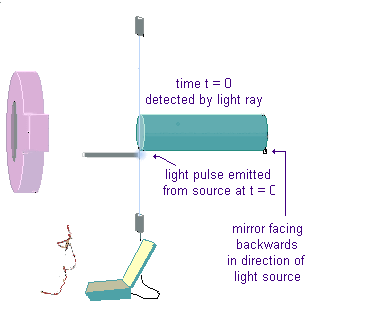
The observer uses the vertical light beam, as shown on the left, to set a clock in his frame to zero and, at this time, a pulse of light is also sent from behind the magnet and later reflected backwards off the mirror at the front of the magnet, as illustrated on the right. This is used as a method to measure the length of the moving magnet, using the Lorentz transform, as follows (Actually, the vertical light emitter, and its detector, should be mounted in such a way that the time taken for the vertical light beam to go from emitter to detector would be as close to zero as possible. Since this would make the illustrations less clear, the arrangement shown should be regarded as being for illustration purposes only, with the vertical light beam being presumed to have an actual arrangement that would reduce its transit time to be as close to zero as possible):

The Lorentz transform for distance in the direction of motion is, as usual,

x' = γ(x - vt)

in which v is the velocity of the magnet and

γ = 1/(1-v²/c²)^1/2.

In the illustration on the right, the rear end of the magnet represents the origin of the inertial frame of the moving magnet, from which x' is measured, x' therefore actually being the length, L', which is the original, or 'proper', length of the magnet. The encounter between the light pulse and mirror on the front of the magnet is the event at a distance, x, in the observer's frame, from the position of the rear end of the magnet at t = 0.

Thus we have

L' = γ(x - vt) or (1/γ)L' = (x - vt)

Thus, (1/γ)L' is the measured length of the magnet in the stationary frame, which is less than its 'proper' length in its own, moving frame.

It can be assumed that, at any time, t, after t = 0, the rear end of the magnet is always at a distance vt from its position at t = 0, since this is a stationary frame specification that expresses the definition of the velocity of the moving frame relative to the stationary frame.

These calculations form part of the data collected locally, by the local observer. A crucial property of such an experimental setup will be that it is translationally invariant in space, as discussed below.

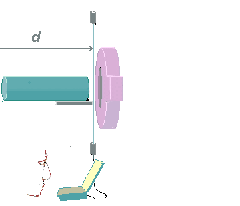
Let d, as shown, represent a distance that describes the location of the experiment within the stationary observer's frame of reference. The other end of this distance can be any distant fixed location in the observer's frame, beyond the region shown in the

illustration. It is self-evident that any data collected by the observer is completely independent of the value of the distance, d.

If, now, the experiment, together with the observer, and his apparatus, were all moved and set up in exactly the same manner as before, in the same inertial frame as before, at an arbitrary distance, d', replacing the distance, d, this could not in any way make any difference to the experimental data collected by the observer. I refer to this fact by saying that the experiment is translationally invariant within the stationary observer's inertial frame. This is something that is self-evident, and requires no further proof or demonstration.

THAT THIS EXPERIMENT IS TRANSLATIONALLY INVARIANT:

Let there be two identical experiments set up, in the stationary frame, with two local observers, with identical sets of apparatus. This arrangement is essentially no different to that involving the two identically accelerated rocket ships in Bell's Spaceship Paradox.

The previous argument, establishing the translational invariance of the experiment in the observer's inertial frame, is sufficient to prove that the two sets of data collected by the two observers must be identical in all respects, not only from the perspective of the stationary frame observers, but also by any measuring instruments that might be set up, in the moving frame, on the magnets themselves.

If each observer, in addition, has a clock, synchronised with an identical clock in the possession of his fellow observer, these clocks can be used to prove that all the events, or items of experimental data, associated with the

identical experiments, were simultaneous in the single reference frame of the observers.

Thus, the time, t = 0, occurred simultaneously in both experiments. Both light pulses encountered the front mirrors of both magnets simultaneously. The values of the times, t, associated with these events, were simultaneous, and the distances, vt, of the rear ends of the magnets from their local origins at t = 0 were also simultaneous. Likewise, if each magnet has a clock mounted on it, that are synchronised with one another in the stationary frame before the magnets begin to move, then the values of the times, τ, shown on the moving clocks will always be the same, whether the time is recorded in the stationary frame or is recorded in the moving frame and then transmitted to the respective stationary frame observer.

All this is established simply by the translational invariance of the original single experiment.

THAT DUPLICATION OF THIS EXPERIMENT, AT ANY SPATIAL DISTANCE FROM IT, MUST PRODUCE TWO SETS OF IDENTICAL EXPERIMENTAL RESULTS:

THAT A SPACELIKE COMPARISON OF THE TWO SETS OF DATA SHOWS NO RELATIVISTIC FORESHORTENING OF THE DISTANCE BETWEEN THE MAGNETS:

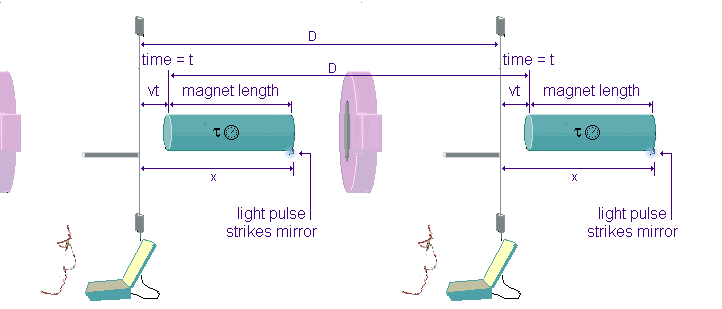
The two experiments have their local origins, in the inertial frame of the observers, at a distance, D, apart, as shown. It has been demonstrated that, the experiments being identical, the rear ends of the magnets are each simultaneously at the same distance, vt, from these origins.

These facts lead to the inescapable conclusion that the rear ends of the two magnets must also be a distance, D, apart.

Since, however, when the magnets were at rest before the start of the experiment, they were also, by definition, identically located relative to the local origins, they must also have been at a distance, D, apart. Therefore, even when the magnets are moving together, at velocity v relative to the inertial frame of the observers, a spacelike comparison of

the locally collected experimental data shows them to be still at a distance, D, apart.

That is, this distance does not display any relativistic foreshortening effect due to the motion of the magnets.

During the period of acceleration also, the magnitudes of the velocities of the magnets will be always simultaneously the same, so that at no time can the magnets ever be considered to be other than at a distance, D, apart.

These results refer specifically to the context of the spacelike comparison of events, and are justified entirely by the translational invariance of the experiment within the inertial frame of its observer.

Statement of the Basic Argument:
The following is the argument used to supposedly answer the lack of foreshortening of the distance between the magnets, and applies originally to the lack of foreshortening of the distance between the spaceships in Bell's Spaceship Paradox.

During the period of acceleration, the velocities of the magnets, viewed from the stationary frame, will be always simultaneously the same, so that at no time can the magnets ever be considered to be other than at a distance, D, apart. However, it has been argued that, in the reference frame of the magnets, the proper distance apart of the magnets is stretched, during acceleration, in a manner to compensate for a length contraction effect, such that no length contraction will be visible in the stationary frame, even though, in reality, it has actually occurred. That is, since the length contraction of a proper distance, D, is (1/γ)D, a compensatory stretching of the proper distance to a distance γD in the moving frame would produce a length contracted distance, as measured in the stationary frame, (1/γ)γD=D, thus creating the appearance of no length contraction in the stationary frame.

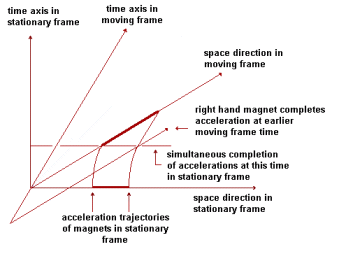
This proposal relies on the principle that one can regard the final, moving frame, into which the magnets will be accelerated, as something pre-existing, in spacetime, with a pre-existing nonsimultaneity relationship between it and the stationary frame. It is then claimed that, from the perspective of this moving frame, the accelerations did not appear to begin simultaneously in the stationary frame, so that the acceleration that started earlier caused the front object to be further ahead than it would have been had they started simultaneously, thus producing a resultant stretching of the distance between the magnets on arrival in the moving frame. Alternatively, from the perspective of the stationary frame, the right hand magnet is said to arrive in the moving frame before the left hand magnet, so that it will be further ahead in the moving frame, when the left hand magnet arrives, than it would have been had they arrived simultaneously, thus stretching the original distance between them.

The Minkowski spacetime diagram illustrating the occurrence of the stretching of the distance is shown below.

The answer to this proposal relies on two well known fundamental principles in modern physics, as follows:

1) The principle of translational invariance of an experiment in space, as mentioned already.

2) The principle in Special Relativity that no causal connecting principle can connect two events faster than the speed of light.

If the above argument is true, it would have to be manifested by some difference in the acceleration data of one object compared to that of the other, since the accelerations were simultaneous, according to data that would be collected by instruments mounted on the magnets, when they started. Completely identical sets of data would reflect, instead, the original simultaneity of the start of the accelerations in the two experiments. That is, clock data from the two experiments would show a simultaneous start time, 0, in the stationary frame, and a simultaneous arrival time, τ, in the moving frame, after both magnets had travelled identical distances, viewed from either frame. A nonsimultaneity effect would have to produce two different values of the arrival time, τ, in the moving frame, somewhere in the experimental data.

The principle of translational invariance of an experiment in space, however, specifies that, in fact, all items of time data, as well as all others, will be identical for both experiments. That is, simply carrying out an experiment at a different location in space cannot modify any item of experimental data associated with the experiment.

Since no items of data can locally detect the working of a nonsimultaneity relationship between the two frames, it might be suggested that this relationship operates as a relationship between the two experiments, rather than as a locally expressed difference between them.

However, since a compensatory stretching of the proper distance would require stretching to a distance γD in the moving frame, the stretching is a function of the distance apart, D, of the two experiments. The supposed nonsimultaneity will therefore have the effect of creating the equivalent of a mathematically expressible, faster-than-light connecting principle between the two experiments. In addition, it does not appear that such a connecting principle, if it were possible, would be able to avoid causing a difference in the data collected locally by the experiments.

First Defence of the Argument:
One might try to get around this by proposing that the nonsimultaneity effect works like a kind of 'landscape effect', which does not require a faster-than-light connecting principle. That is, to use a crude comparison, if person A climbs hill A and person B climbs hill B, which are sloped differently, then the spacelike distance between A and B can stretch without any faster-than-light connecting principle being involved.

First Defence Answered:
This effect, however, is achieved by a difference between the experiments, created locally by each experiment, which therefore establishes the effect without the operation of a connecting principle. Another way to express this is that the hill-climbing experiment is not translationally invariant within the landscape.

This explanation cannot be applied to the magnet experiments, which are identical in all respects, and also translationally invariant in space. A landscape explanation will therefore not be able to explain the claimed difference between the accelerations of the magnets, and stretching of the distance between them.

Second Defence of the Argument:
Another attempt to get around the problem, which has been suggested, is to propose that the landscape effect exists, but is not detected by the local experimental data. That is, a combination of accelerometer and magnet on-board clock data, along with distance travelled, which are identical for both experiments, does not reflect the true nature of the transition of the magnets from one frame to the other, and cannot be used to specify the true arrival times in the moving frame, which are claimed to be simultaneous in the view of the stationary frame, but different within the moving frame.

Second Defence Answered:
This approach, however, confers an arbitrary preference on some items of data as being valid, compared to others, in order to satisfy theoretical requirements. That is, the readings of stationary frame clocks are specified to be valid, but the readings of magnet on-board clocks are discounted as invalid in specifying identical arrival times in the moving frame. Identical magnet accelerometer data, specifying identical accelerations, is thus also discounted.

We thus have, here, the working of an undetectable, phantom spacetime landscape, that is able to selectively invalidate items of experimental data, even though the theory of Special Relativity, as a whole, is grounded in problems relating to experimental data. Such a situation has all the appearances of a theory that is being upheld in the face of contrary experimental evidence. The experimental evidence, even though involving thought experiments, is unquestionable, if the two principles of translational invariance of the experiments in space and the impossibility of faster-than-light connection between them are upheld.

Conclusion:
In view of the above arguments, it is impossible to postulate a stretching of the distance between the magnets at all, never mind in accordance with a function γD, without violating the principle of translational invariance of the experiments, or that of the spacelike disconnection between them, and this should be considered to exclude any possibility of the existence of an associated, hidden length contraction effect.

It might, perhaps, be argued that, if this conclusion is correct, and the experiment displays neither a length contraction effect in the stationary frame, nor a stretching of the distance in the moving frame, the Special Relativistic prediction of a length contraction effect is discounted altogether.

This, however, need not be the case. The distance apart of the magnets, in the stationary frame, is being measured in a spacelike manner, without sending a pulse of light from one magnet to the other in order to examine the distance between them. I therefore propose that the answer must be that measurement of the distance by using a pulse of light would, in fact, detect a length contraction effect between the magnets. This proposal is discussed below.

AGAINST ARGUMENTS SUGGESTING A STRETCHING OF THE DISTANCE
BETWEEN THE MAGNETS, AS MEASURED IN THE MOVING FRAME
(Which is the Standard Answer to Bell's Spaceship Paradox):

AN EXPERIMENT ILLUSTRATING THE LIGHTLIKE
COLLECTION OF DATA BY A SINGLE OBSERVER:

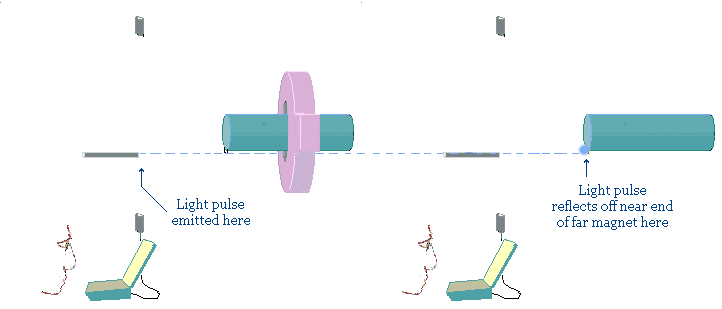
The illustration shows two identical experiments, separated by a distance that isolates them from one another. The left hand observer is gathering data in a lightlike manner from two spacelike separated events. These events are the positions of the rear ends of the two magnets. Light is sent from the left hand experiment and reflected off the rear mirror on the magnet of the right hand experiment.

The important event in this experiment is the location of the rear end of the right hand magnet, based on data gathered remotely, in a lightlike manner, by the left hand observer. This time, the left hand observer sends a pulse of light, at time, t = 0,

which reflects off the rear end mirror of the other observer's magnet, instead of the front mirror of his own magnet, as previously. Instead of calculating the length of his own magnet, as before, the left hand observer now calculates the distance apart of the rear ends of the two magnets, using the same Lorentz transform equation as before.

The left hand observer is not using a pulse of light to find out where the rear end of his own magnet is, because he already knows that it is always at a distance vt from where it was at the time that is defined as t = 0.

THAT THE LIGHTLIKE COMPARISON OF EVENTS BY THE LEFT HAND OBSERVER
DISPLAYS A FORESHORTENING OF THE DISTANCE BETWEEN THE MAGNETS:

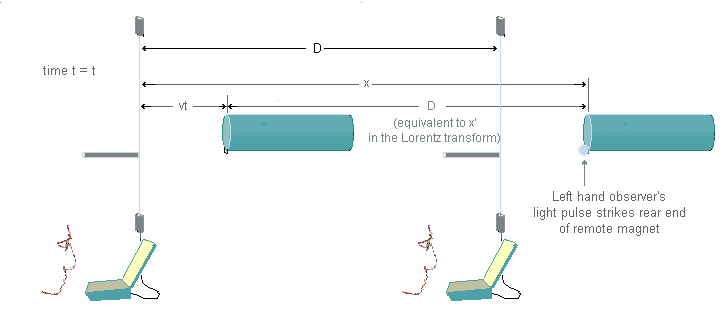
The illustration shows the method used by the left hand observer to measure the distance from his origin, defined by the time, t = 0, in his reference frame, to the rear end of the second observer's magnet.

At the moment that the time, t, is set to zero, as before, the first observer's apparatus sends a pulse of light to a backwards facing mirror, this time on the rear end of the second magnet, rather than on the front end of his own magnet, as previously. Time, t, will now be the time that his light pulse encounters the mirror on the rear end of the second magnet, which constitutes the event he will examine.

At this time, the rear end of his own magnet will be, as always, at a distance vt from the origin in his frame, that is, where it was at t = 0.

The origin of the moving reference frame, now

regarded as containing the two magnets moving at velocity, v, is still the rear end of his own magnet, and the distance, x', in the Lorentz transform is therefore now the measured distance, D, between the rear ends of the two magnets. Thus, the Lorentz transform

x' = γ(x - vt)

becomes

D = γ(x - vt) or x - vt = (1/γ)D

The results obtained by the left hand observer, for whom, this time, all relevant data of both experiments is obtained by him entirely in a lightlike manner, will indicate that the distance between the rear ends of the magnets is foreshortened from the proper distance, D, to (1/γ)D.

A comparison of the results obtained from the foregoing experiments shows that the results obtained from an examination of two particular events in a moving inertial frame are not independent of the manner in which the data was gathered.

These results make it clear that, in the case of spacelike separated events, a spacelike comparison of the events produces results that disagree with those produced by a lightlike comparison of the same events. The data gathered in a spacelike manner does not display a foreshortening of the distance, within the moving frame, between these events, whereas the data gathered in a lightlike manner does.

A similar result will be obtained in respect of nonsimultaneity effects relating to the two events. A spacelike comparison of moving clocks, by two observers in a stationary frame, located immediately opposite the present locations of the two clocks, will show both clocks to be time dilated in an identical manner, and be synchronised with one another, or will be seen to simultaneously display the same time in the moving frame.

However, according to a lightlike comparison of the the times on the clocks by the left hand observer,

who will receive information about the time on the second clock by receiving a light signal from it, both clocks will not appear to be equally time dilated, as the second magnet clock will appear more time dilated than the first, The clocks will thus not appear to be synchronised, or to show the same time simultaneously in the moving frame, from the perspective of the stationary observer.

The foregoing argument, that reveals a distinction between the the results of the spacelike and lightlike examinations of the same events, establishes that the transformation equations of Special Relativity do not reveal the independent nature of an underlying spacetime. If such were the case, then there could be no difference between the results of spacelike and lightlike examinations of the same events. The conclusion consequent to the difference produced by the lightlike examination of events must be that such results reveal something about the nature of light itself, on which the results depend, rather than on any independent feature of an underlying spacetime. This automatically calls into question the interpretation of the Minkowski equation as representing any real, underlying spacetime, and the similar interpretation of the spacetime diagram used to illustrate it.

CONCLUSIONS:

© Alen, March 2007; update Dec 2010.
June 2019 - re-engineered to display properly on Chrome and Firefox.
alen.1@bigpond.com