A CRITICAL EXAMINATION OF THE TWINS PARADOX
IN SPECIAL RELATIVITY
The Twins Paradox is a consequence of the Lorentz transformation equations in the context of Special Relativity, in which an observer considers a moving clock to run slow, and hence a moving observer to appear to age more slowly. Because of this, each of two twin observers in relative motion regards the other as being the one in motion, and each, therefore, expects the other's clock to be running more slowly, and the other to be younger. Clearly, of course, two clocks cannot each be slower than the other, and two persons cannot each be younger than the other.
The standard attempt to solve this contradiction involves identifying a difference between one twin and the other. In the case, for example, where one twin remains on earth, and the other travels to a nearby star and back, one of them engages in using his engines to create accelerations and decelerations during the round trip, while the other never fires his engines, and does not accelerate, and this is used to apparently prove that only one twin is to be regarded as younger than the other.
What can be said against this is that the travelling twin sees the earth, and the star, and the whole galaxy, to be the accelerated reference frame, rather than himself. He sees the Earth, the stationary twin, and the star, all together leaving his stationary reference frame and returning, which is a perfect and contradictory counterpart of what the stationary twin sees from his earthbound point of view.
The answer usually given to this is that the twin that fires his engines can detect his acceleration from within his reference frame, by means of an accelerometer, for example, whereas the other twin cannot detect any acceleration within his frame. A significant difference between the twins is presumed to have been established, in this way, that will be sufficient to solve what is regarded as only an apparent paradox.
I shall proceed, for the moment, with an analysis of the above apparent explanation, which involves the view that the travelling twin follows a different 'spacetime path' than the stationary twin, between the event when he leaves earth and the event when he returns. Such a different spacetime path, involving a different accumulated total distance in the direction of a time coordinate, allows the travelling twin to accumulate a lesser total time on his clock than the stationary twin. This view is created mathematically by integrating or, in other words, accumulating, clock times to show that the accelerated twin accumulates less time on his clock than the other. I intend to show here, however, that this mathematical procedure cannot be made to work, even at the purely mathematical level, apart from any interpretation.
THE PARADOX AND THE STANDARD METHOD OF SOLVING IT:
Start with the Minkowski spacetime time dilation equation, or Lorentz transformation time dilation equation, which are equivalent:
c2dτ2 = c2dt2 - dx2 - dy2 - dz2
in which dx, dy, and dz specify spatial distances, in the stationary frame, through which the travelling twin moves in stationary frame time dt. dτ is a time interval on the travelling twin's clock, corresponding to the time interval dt in the stationary frame. This can be written as:
c2dτ2 = c2dt2 - ds2
In which the resultant distance, ds, is obtained from ds2 = dx2 + dy2 + dz2, and from which we can get
dτ2 = dt2 - ds2 = (1/γ)2dt2
where γ = (1 - v2/c2)-1/2, or 1/γ = (1 - v2/c2)1/2,
and c = 1
which gives the Lorentz time dilation equation
dτ = (1/γ)dt
dτ, here, is one small time interval recorded on the moving twin's clock (while travelling to the star and back). It is also the value that will be associated with the moving clock by the twin that remains stationary on the earth. And it is equally the value
that will be understood by any other observers moving with different velocities, and all will agree on the value of dτ.
This also includes the case of an observer moving with zero velocity relative to the travelling twin; that is, it includes the travelling twin himself. dτ is thus also the time the travelling twin, as an observer at zero velocity, associates with his own clock, and will be the time he actually sees on his own clock, if his clock was set to zero at the beginning of the measured time interval. dτ is thus an invariant, i.e. independent of any relative velocity, and is referred to as the travelling twin's own 'proper time'.
dt, however, is the corresponding time measured on his own stationary clock by the twin on earth, and also by any of the other observers clocks, which are equally stationary in their reference frames, and each, using his own version of this equation, will measure a different value of dt according to his own clock, depending on his velocity relative to the travelling twin. That is, dt is not an invariant, but depends on velocity. If, for example, all clocks are physically identical, and dτ represents one tick of the travelling clock, other observers might measure 1.x, or n.x ticks etc on their clocks, depending on the twin's velocity relative to each separately. For the travelling twin himself, of course, γ=1, and his dt = dτ.
SETTING UP THE EQUATION TO BE INTEGRATED:
To get the total time accumulated by the travelling clock, the Lorentz equation is used to integrate dτ in terms of dt as
dτ = (1/γ)dt
and this is less than the accumulated time on the stationary clock, which is said to be simply dt because, for the stationary clock, since its velocity in its own frame is zero, γ = 1 , and (1/γ)dt = dt.
The problem with this is that the first of these equations cannot be integrated as it stands. If I want to integrate a function f(x)dx, I cannot do so in the normal way if dx is not an constant interval, but is itself a function of x. Instead, dx must first be converted as, for example, dx(x) = f'(x)dx', where dx' is a constant interval, independent of x. Thus, I must integrate f(x)f'(x)dx'.
Such a situation can occur in an integration like dy = f(x)dx, where dy = f(x)dx, if dy is not allowed to function as a resultant value, or as a dependent variable, but has its value fixed in advance. For the equation dτ = (1/γ)dt, in which
dτ = (1/γ)dt, dτ is specified in advance as a constant, independent of γ, and therefore cannot be regarded as a resultant value, or dependent
variable. Since acceleration can be regarded as a stepwise series of inertial reference frames, each at a slightly different velocity, the values of dt change incrementally with velocity, since they are related to dτ as an invariant, as mentioned before. Therefore the integral equation must really be written
dτ = (1/γ(v))dt(v)
or it can be written
dτ = (1/γ(t))dt(t)
A way to get around this is to convert dt to an interval that, like dτ, will remain an invariant, independent of γ, throughout the summation. Then the relationship between dτ and dt will effectively be the same as if dτ was a dependent variable.
An attempt at an objection to this may be raised, however, in that the above equations involve a comparison between dt and (1/γ)dt, if the same dt is considered to be used in both. Therefore, what does it matter if dt is a function of velocity, since it is the same measure used for both integrals, and therefore the comparison between them is valid without the need to convert dt to an interval independent of velocity.
This will not work mathematically, however, because of the fact that the term 1/γ is also a function that does not remain constant. It may be possible to argue that this approach can be validated by regarding the integral in terms of a stepwise summation, rather than an integral. I will however proceed, instead, to consider the nature of the integration (1/γ(v))dt(v) by converting dt to a constant interval, for a reason that will become evident in the following argument.
THE IMPOSSIBILITY OF INTEGRATING THE EQUATION, AS WRITTEN:
To convert dt, start with a second Minkowski, or Lorentz transformation, equation and, this time, arbitrarily specify dt to be a constant interval, dt', independent of velocity. We then have two transformation equations, as follows:
dτ2 = dt2 - ds2 or dτ = (1/γ)dt,
which is the same equation as before, with dτ independent of velocity, and
dτ'2 = dt'2 - ds'2 or dτ' = (1/γ)dt',
which is the new equation, with dt' now independent of velocity.
The equations are to be considered written in terms of the same velocity, so that γ remains the same. In the second equation, since dt' is specified to be independent of velocity, dτ' must now be dependent on velocity, because γ is. One might therefore ask, "what does dτ' actually mean, or refer to?" Since this will not be important in the following calculation, let us dispose of this question by saying "let it mean nothing in particular, or nothing of importance".
Now, divide the two equations into one another, to obtain
dτ'/dτ = dt'/dt, which leads to dt = (dτ/dτ')dt'
which converts dt to an equation containing the constant interval dt'. Putting this in the original equation (dτ = (1/γ)dt), we have
dτ = [(1/γ)(dτ/dτ')]dt'
It will not be necessary to go further into this equation, but only point out that, since dτ and dt' are both independent of velocity, the term in square brackets must be independent of velocity also. Let us put it = K
(1/γ)(dτ/dτ') = K and, consequently dτ = Kdt'
Now, let us specify that dt' represents, by definition, the current, or present, time interval on my clock, if I am the stationary twin. By this I mean that, if the clock has been set to zero at the start of the measured interval, dt' will represent the time I currently actually see on my clock. I can specify dt' in this way, because the effect of changing the definition of dt' is only to give a different value to K, but leave the equations the same as before. So I can specify dt' to be whatever I wish, provided it is not dependent on velocity. dτ, as before, can also be arbitrarily defined to represent the time a moving observer currently sees on the moving clock, as the equations are created, or specified, independently, and, also, clocks are set to zero at the start. Let us also specify that both clocks are physically identical. What, then, is the value of K?
The Minkowski metric equation, and the Lorentz transformation equation, are both such that they are valid for an infinitesimal velocity, and a velocity of
zero; that is, for a velocity, v = 0, and ds = 0, in the Minkowski equation, and for γ = 1, in the Lorentz transformation equation. Therefore, in the equation (1/γ)(dτ/dτ') = K, if we have the velocity, v = 0, we will have (1/γ) = 1, and K = dτ/dτ'.
When both clocks are at rest together, and the relative velocity is zero, if both clocks are identical, the lengths of their ticks are identical, and therefore dτ = dt', and, since dτ = Kdt', we must have K = 1. This is consistent with the original definition of these times as the current time intervals on both clocks for both observers. Only if the clocks were differently calibrated would the factor K have a value other than 1. If K = 1 when the clocks are at rest, it must be true at any velocity, since K is independent of velocity. We can therefore say that dτ = dt' represents the current proper time for both of us, from the definition of dt', no matter what our relative velocity. And if this applies to us, it applies likewise to all inertial frames in relative motion and, thus, the proper time for any is a universal proper time for all.
If K = 1 in the equation
(1/γ)dτ/dτ' = K
we will have
(1/γ)dτ = dτ'
and, since dτ/dτ' = dt/dt'
(1/γ)dt = dt'
Since dτ and dt' refer to current clock times for the relevant observers, it follows that dτ' and dt do not. Thus, in a single Minkowski equation, both time intervals are not current time intervals for the observers in the two frames. This result is consistent with the direct proof of this given in the link at the bottom of this page.
What, then, is to be said of the time interval dt in the equation dτ = (1/γ)dt, for dt depends on the velocity and is > dτ, and hence also > dt', which is my current proper time? It follows that, since dt refers to an interval on my clock that is larger than the interval that specifies my current time, it penetrates into my future and, although it can be calculated, it cannot be immediately read on my clock. It further follows that, where we refer to an accumulated time which is given by the integral, dt, specifying dt to be the same as it is in the equation dτ = (1/γ)dt, this time refers to an accumulated time that also I will only encounter, or observe on my clock, in my future. It is always greater than the actual accumulated time I can read on my clock, which is dt'.
My clock, or any clock, accumulates only its own current proper time, and not a greater time. That is, all clocks of all observers accumulate the same current proper time, independently of velocity, and changes in velocity, and 'spacetime paths' considerations have no effect.
MAKING THE EQUATION INTEGRABLE ALSO MATHEMATICALLY PROVES THE EXISTENCE
OF A UNIVERSAL CURRENT PROPER TIME FOR ALL OBSERVERS IN RELATIVE MOTION:
The explanation referred to at the start, which depends on the integration dτ, as the accumulation of the time on my travelling twin's clock, being less than the accumulated time, dt, on my clock, cannot be correct, because the greater accumulated time, supposedly appearing on my clock, dt, will not be visible until some time in my future, after my travelling twin has already arrived home. When he does arrive home, he will see the accumulation of my current proper time dt', which will be the same as the accumulation of his current proper time, dτ.
In general, the value dt is only a projection of a time interval into a 'stationary' reference frame, and is not the actual, present time in that frame. Though it can be useful for transformation purposes, in the usual way, it has no immediate physical significance.
The universal current proper time concept thus immediately disposes of the twins paradox. The twins really always remain the same age, no matter how they may see one another when in relative motion, and will again see one another to be the same age when they come to rest in the same reference frame once more.
Let us ask, "how do the twins see one another when in relative motion?"
To attempt an answer to this, consider, again, the first equation
dτ = (1/γ)dt
It has been shown above that dτ = dt', the current time on my own clock, if I am the stationary twin, and dt > dt' is a time interval partially penetrating into my future. Consequently, although dτ, on the travelling clock, can be inferred, and hence dt calculated, it makes no sense to say that I can actually see dτ, since I cannot actually see dt.
Consider, therefore, the second equation
dτ' = (1/γ)dt'
Here dt', my current proper time, is a time I always actually see on my clock, and therefore it makes sense to suppose that, if I look at the time on a moving clock, I will see dτ', and not dτ, although the moving observer himself sees dτ.
This means that I cannot see the moving clock as it
really is in the universal current proper time, because I see dτ' < dτ, which is less than the current time, and thus the moving clock appears to run slow.
It follows that the invariant dτ, though all observers can agree on its value, as usual, is not the value that stationary frame observers can actually see on a moving clock, and each of them sees the moving clock to read a different time, depending on the velocity of the clock relative to him.
Since, however, there is only one moving clock, how do I see it differently to what it really is? In answer to this, I make the suggestion that I see it not directly as it is, but as it was. That is, I see it via a present manifestation of its past history.
When, therefore, I see my travelling twin to be younger than myself, and he sees me to be younger than him, we are each seeing the other as he was, and not as he is. When, however, we decelerate in order to come to rest again in the same reference frame, we will each see the other aging rapidly during the deceleration until, when at rest again together, we see one another to be the same age again as, if fact, we really always were. This applies independently of whether only one of us engaged in acceleration, or both.
This interpretation also serves to explain how an observer sees a moving clock to 'run slow', Since an observer sees a moving clock reading a progressively earlier and earlier historical time, he has the impression that the clock is running slow. A possible way to speculate as to what mechanism might enable a clock to currently display an earlier, historical time, is to imagine that the observer is observing the clock via a scale change in the direction of the time dimension though not, of course, as something that actually exists in the moving frame.
I would add that this 'past history' interpretation should not be thought to mean that, by interfering with my travelling twin's reference frame, I can alter his past history. Even if I were able to create an effect of some such kind, I still could not disturb his actual past history. This can be seen immediately in that, if I changed a person's past, the fact that I changed it would itself be a historical fact, necessitating the preservation of the original past as well.
WHAT, THEN, OF THE TWINS PARADOX?:
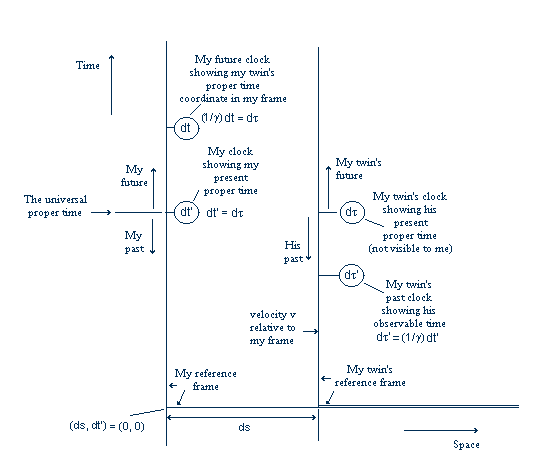
In this figure, both clocks, showing the universal time, coincided spatially at the origin of my frame, at (0, 0), and are travelling up the page in their reference frames in the time direction. Strictly, I suppose, they should have complete reference frames travelling in the time direction, within a fixed spacetime coordinate frame, but I think that the illustration is sufficiently meaningful as it is, if this is understood.
The above figure does not display a full description of the relationship of the inertial reference frames, as it does not display the Lorentz-Fitzgerald contraction effect and illustrates, immediately, the time relationships of two clocks only.
My reference frame is used as a spacetime coordinate frame in which my twin's clock is moving in space and time, and mine is moving in the time direction only, and both clocks spatially coincide at (ds, dt') = (0, 0), at the coordinate frame origin.
If both reference frames have arrays of spatially distributed, synchronised clocks, the time relationships shown in the illustration will apply in respect of the locations of clocks in the two arrays which were spatially coincident when the two clocks in the illustration were spatially coincident, if such clocks are observed at those locations.
Thus, if I look at another clock in my twin's frame which was at (s, 0) from my position when I was at the origin, (0, 0) and is at (s+ds, dt') at the time shown in the illustration, I cannot say that I will see such a clock also showing the same observable time indicated in the diagram dτ', when viewed from where I am.
The figure thus refers only to the clocks actually shown, but is also valid for the locations of other synchronised clocks that were spatially coincident at the same time that these were.
Considering the phenomenon of the extended lifetimes of muon particles adds a further dimension to the above understanding of a universal current proper time. Muon particles are created, at high velocity, in the upper atmosphere, by cosmic rays from space. Their lifetimes are such that they should never last long enough to reach the surface of the Earth. The fact that they do is explained by the consideration that, at high velocity, they are seen to age more slowly, as specified by the Lorentz transformation equation, and their thus extended lifetimes enable them to last long enough to reach the surface of the Earth.
The above interpretation, involving a universal current proper time, would appear to specify that a muon particle really does decay in the upper atmosphere, in the time in which it would at zero velocity. The muon particle that reaches the surface
of the Earth is explained as an extended view of its past history. This, however, clearly cannot be merely a window into its past because, in its past, it never did reach the surface of the earth. This extended view of its past must clearly exist, in some way, as a real particle, independently of its original past. I have therefore referred to it as a 'present manifestation' of its past history. But, if it becomes necessary to deal with a paradox involved in interacting with a reality via its past history, it may have to be considered as to whether the muon lifetime may be a specification restricted to its own inertial frame. That is, it may have to be considered whether or not the muon may be simply displaying different lifetimes in different reference frames, possibly determined, in advance, by the target that will intercept it. But I need not attempt to argue this here, in the sense that the foregoing argument does not depend on my doing so.
ON THE EXTENDED LIFETIME OF MUON PARTICLES:
The result of the Hafele-Keating experiment would appear to contradict the above conclusions regarding a universal current proper time, in that it is reputed to show that a clock, taken on an aircraft around the world, and compared with a similar clock left stationary on the earth, shows a change in its accumulated time predicted by the 'spacetime paths' explanation of the twins paradox. The universal current proper time explanation, above, predicts that, excluding effects of gravitation etc., the travelling clock will always show the same time as the stationary clock, when it returns.
An engineer who obtained the original data of the experiment has shown that the result is severely flawed. In fact, if it shows anything, the experiment tends to show that the travelling clock does not accumulate a time difference, and rather supports than contradicts the universal current proper time
interpretation.
The section heading contains a link to the analysis by the engineer (AG Kelly).
By this reference to the Hafele-Keating experiment, I do not intend to make the case that it should be regarded as a satisfactory experimental proof of the existence of a universal proper time. In my view, a more rigorous experiment would be required to establish a definite experimental proof. The Hafele-Keating experiment, by its nature, is large scale and poorly controlled. Every jolt on a clock, for example, and every kind of acceleration and deceleration, throughout the flight, will produce an unpredictable and unmeasured, acceleration derived modification to the accumulated time displayed by the clock, which will remain on the clock after the experiment is concluded.
© Alen, March 2007; update Dec 2010.
2019 - re-engineered to properly display on Chrome and Firefox.
alen.1@bigpond.com
Material on this page may be reproduced
for personal use only.